مهارات التفكير العليا
المساحات والحجوم
تبرير: أجيب عن الأسئلة الثلاثة الآتية تباعاً:
(22) أجد مساحة المنطقة المحصورة بين منحنيي الاقترانين: .
(23) أجد المساحة المحصورة بين منحتيي الاقترانين: .
(24) أجد مساحة المنطقة المحصورة بين منحنيي الاقترانين : ، حيث عدد صحيح أكبر من أو يساوي 2، مبرراً إجابتي.
أولاً إذا كان n زوجياً
يتقاطع المنحنيان عند
ثانياً إذا كان n فردياً
يتقاطع المنحنيان عند
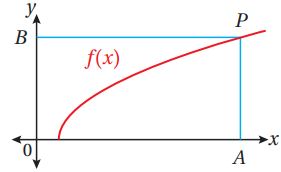 تبرير: يبين الشكل المجاور منحنى الاقتران: ، حيث: . إذا كانت النقطة تقع على منحنى الاقتران ، حيث يوازي المحور ، و يوازي المحور ، فأجد كلاً مما يأتي:
تبرير: يبين الشكل المجاور منحنى الاقتران: ، حيث: . إذا كانت النقطة تقع على منحنى الاقتران ، حيث يوازي المحور ، و يوازي المحور ، فأجد كلاً مما يأتي:
(25) مساحة المنطقة المحصورة بين منحنى الاقتران ، والمستقيم والمحورين الإحداثيين.

نقسم المنطقة المطلوب حساب مساحتها إلى قسمين برسم المستقيم x=1، ونجد المساحة كما يأتي:
(26) مساحة المنطقة المحصورة بين منحنى الاقتران ، والمستقيم ، والمحور .
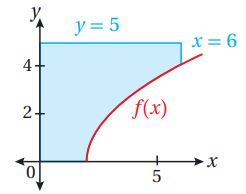 (27) تبرير: بين الشكل المجاور المنطقة المحصورة بين المحورين الإحداثيين في الربع الأول، ومنحنى الاقتران: ، والمستقيمين: . أجد حجم المجسم الناتج من دوران المنطقة حول المحور ، مبرراً إجابتي.
(27) تبرير: بين الشكل المجاور المنطقة المحصورة بين المحورين الإحداثيين في الربع الأول، ومنحنى الاقتران: ، والمستقيمين: . أجد حجم المجسم الناتج من دوران المنطقة حول المحور ، مبرراً إجابتي.
نقسم المنطقة إلى قسمين برسم المستقيم x=2، ونجد الحجم كما يأتي:
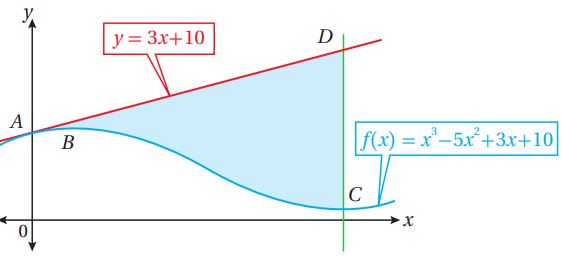 تبرير: يبين الشكل المجاور منحنى كل من الاقتران: ، والمستقيم: . إذا مر المستقيم ومنحنى الاقتران بالنقطة الواقعة على المحور ، وكان للاقتران قيمة عظمى محلية عند النقطة ، وقيمة صغرى محلية عند النقطة ، وقطع الخط الموازي للمحور والمار بالنقطة المستقيم: في النقطة ؛ فأجيب عن الأسئلة الثلاثة الآتية تباعاً:
تبرير: يبين الشكل المجاور منحنى كل من الاقتران: ، والمستقيم: . إذا مر المستقيم ومنحنى الاقتران بالنقطة الواقعة على المحور ، وكان للاقتران قيمة عظمى محلية عند النقطة ، وقيمة صغرى محلية عند النقطة ، وقطع الخط الموازي للمحور والمار بالنقطة المستقيم: في النقطة ؛ فأجيب عن الأسئلة الثلاثة الآتية تباعاً:
(28) أجد إحداثيات كل من النقطة ، والنقطة .
نقطة القيمة العظمى هي:
نقطة القيمة الصغرى هي:
(29) أثبت أن مماس لمنحنى الاقتران عند النقطة ، مبرراً إجابتي.
النقطة A تقع على محور y إذن أحداثياها هما:
ميل المنحنى عند A هو:
معادلة مماس المنحنى عند النقطة A هي (حيث ):
وهذه المعادلة هي معادلة المستقيم نفسها.
إذن، مماس لمنحنى عند النقطة A
(30) أجد مساحة المنطقة المظللة، مبرراً إجابتي.
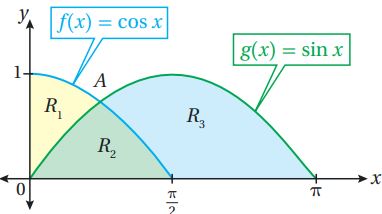 تبرير: يبين الشكل المجاور منحنيي الاقترانين: ، معتمداً هذا الشكل، أجيب عن الأسئلة الثلاثة الآتية تباعاً:
تبرير: يبين الشكل المجاور منحنيي الاقترانين: ، معتمداً هذا الشكل، أجيب عن الأسئلة الثلاثة الآتية تباعاً:
(31) أجد إحداثيي النقطة .
نلاحظ من الرسم المعطى x تقع في الفترة
إذن، إحداثيا النقطة A هما:
(32) أجد مساحة كل من المناطق: .
(33) أثبت أن مساحة المنطقة إلى مساحة المنطقة تساوي: .
إذن:
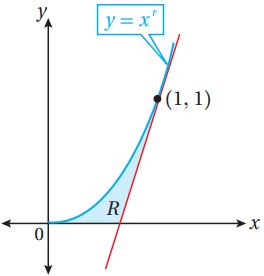 تحد: يبين الشكل المجاور المنطقة المحصورة بين منحنى الاقتران: حيث: ، والمحور ، ومماس منحنى الاقتران عند النقطة (1,1):
تحد: يبين الشكل المجاور المنطقة المحصورة بين منحنى الاقتران: حيث: ، والمحور ، ومماس منحنى الاقتران عند النقطة (1,1):
(34) أثبت أن مماس منحنى الاقتران يقطع المحور عند النقطة .
ميل المماس عند (1,1) هو:
معادلة المماس هي:
لإيجاد المقطع x لهذا المماس نضع y=0 في معادلته:
إذن، يقطع هذا المماس المحور x في النقطة
(35) أستعمل النتيجة من الفرع السابق لإثبات أن مساحة المنطقة هي وحدة مربعة.
مساحة المنطقة R تساوي المساحة بين المنحنى والمحور x والمستقيمين x=0,x=1 مطروحاً منها مساحة المثلث الذي رؤوسه أي أن هي:
(36) أجد قيمة الثابت التي تجعل مساحة المنطقة أكبر ما يمكن.
ولأن تكون قيمة الحرجة
إذن، قيمة r التي تجعل المساحة أكبر ما يمكن هي:
تحد: إذا كان العمودي على المماس لمنحنى الاقتران: عند النقطة (1,3) يقطع منحنى الاقتران مرة أخرى عند النقطة ، فأجد كلاً مما يأتي:
(37) إحداثيات النقطة .
ميل المماس عند النقطة (1,3) هو:
ميل العمودي على المماس عند النقطة (1,3) هو:
معادلة العمودي:
نجد نقاط تقاطع المنحنى والعمودي على المماس:
(38) مساحة المنطقة المحصورة بين منحنى الاقتران والعمودي على المماس، مقرباً إجابتي إلى أقرب 3 منازل عشرية.
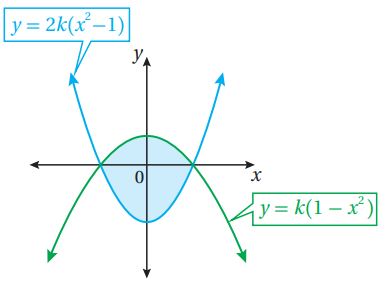 (39) تبرير: المنطقة المظللة في الشكل المجاور محصورة بين قطعين مكافئين، يقطع كل منهما المحور ، عندما . إذا كانت معادلتا القطعين هما: ، وكانت مـساحة المنطقة المظللة هي 8 وحدات مربعة، فأجد قيمة الثابت .
(39) تبرير: المنطقة المظللة في الشكل المجاور محصورة بين قطعين مكافئين، يقطع كل منهما المحور ، عندما . إذا كانت معادلتا القطعين هما: ، وكانت مـساحة المنطقة المظللة هي 8 وحدات مربعة، فأجد قيمة الثابت .






النقاشات