أتدرب وأحل المسائل
المساحات والحجوم
أجد مساحة المنطقة المظللة في كل من التمثيلات البيانية الآتية:
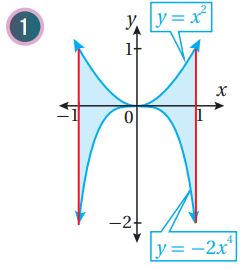
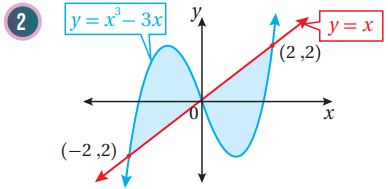
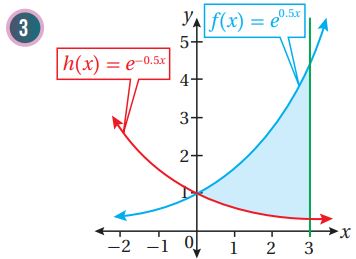
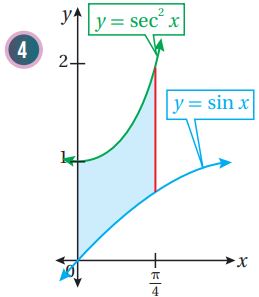
(5) أجد مساحة المنطقة المحصورة بين منحنيي الاقترانين: .
(6) أجد مساحة المنطقة المحصورة بين منحنيي الاقترانين: ، والمستقيم في الربع الأول.
(7) أجد مساحة المنطقة المحصورة بين منحنيي الاقترانين: ، والمستقيم ، في الربع الأول.
نعلم من حلول هذه المعادلة الحل غير السالب:
في الربع الأول يكون بينما ، إذن
(8) أجد المساحة المحصورة بين منحنيي الاقترانين: .
إذن، يتقاطع المنحنيان عند ، ويكون في الفترتين
نجزئ هذا التكامل بسبب تغيير قاعدة حول ، نحسب هذه المساحة على النحو الآتي:
(9) أجد مساحة المنطقة المحصورة بين منحنيي الاقترانين: .
بحساب قيمتي الاقترانين عند عدد بين 2- و0 مثل 1- نجد أن:
في الفترة [2,0-]
بحساب قيمتي الاقترانين عند عدد بين 0 و2 مثل 1 نجد أن:
في الفترة [0,2]
(10) أجد مساحة المنطقة المحصورة بيـن منحنيي الاقترانين، والمستقيمين: .
يمكن استعمال الآلة الحاسبة لمعرفة أن في الفترة
(11) أجد مساحة المنطقة المحصورة بين منحيي الاقترانين: .
في الفترة (0,4)
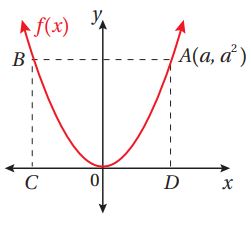 (12) يبين الشكل التالي منحنى الاقتران: . إذا كان إحداثيا النقطة هما ، فأثبت أن مساحة المنطقة المحصورة بين منحنى الاقتران والقطعة المستقيمة تساوي ثلثي مساحة المستطيل .
(12) يبين الشكل التالي منحنى الاقتران: . إذا كان إحداثيا النقطة هما ، فأثبت أن مساحة المنطقة المحصورة بين منحنى الاقتران والقطعة المستقيمة تساوي ثلثي مساحة المستطيل .
من التماثل فإن
لتكن مساحة المنطقة المطلوبة:
مساحة المستطيل ABCD هي:
إذن، المساحة بين المنحنى والقطعة المستقيمة AB تساوي مساحة المستطيل ABCD.
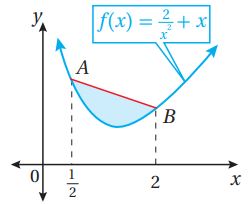 (13) يبين الشكل المجاور منحنى الاقتران: . إذا كان الإحداثي لكل من النقطة والنقطة هو و على الترتيب، فأجد مساحة المنطقة المحصورة بين المستقيم ومنحنى الاقتران .
(13) يبين الشكل المجاور منحنى الاقتران: . إذا كان الإحداثي لكل من النقطة والنقطة هو و على الترتيب، فأجد مساحة المنطقة المحصورة بين المستقيم ومنحنى الاقتران .
ميل AB:
معادلة المستقيم AB:
المساحة المطلوبة هي:
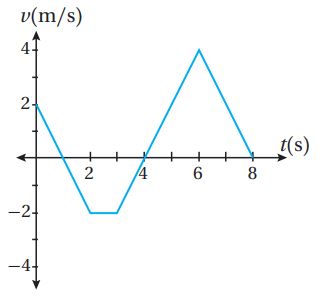 يبين الشكل المجاور منحنى السرعة المتجهة - الزمن لجسيم يتحرك على المحور في الفترة الزمنية ، إذا بدأ الجسيم الحركة من عندما ، فأجد كلاً مما يأتي:
يبين الشكل المجاور منحنى السرعة المتجهة - الزمن لجسيم يتحرك على المحور في الفترة الزمنية ، إذا بدأ الجسيم الحركة من عندما ، فأجد كلاً مما يأتي:
(14) إزاحة الجسيم في الفترة الزمنية المعطاة.
لتكن الإزاحة D
يساوي مساحة المثلث الأيسر في الرسم البياني وهي:
يساوي معكوس مساحة شبه المنحرف في الرسم البياني فهو يساوي:
يساوي مساحة المثلث الأيمن في الرسم البياني وهي:
إذن، إزاحة الجسيم هي:
(15) المسافة التي قطعها الجسيم في الفترة الزمنية المعطاة.
المسافة التي قطعها الجسيم هي:
(16) الموقع النهائي للجسيم.
وبتعويض نجد أن:
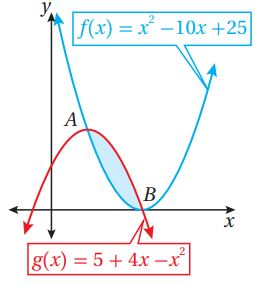 يبين الشكل المجاور منحنيي الاقترانين: ، معتمداً هذا الشكل، أجيب عن السؤالين الآتيين تباعاً:
يبين الشكل المجاور منحنيي الاقترانين: ، معتمداً هذا الشكل، أجيب عن السؤالين الآتيين تباعاً:
(17) أجد إحداثيي كل من النقطة ، والنقطة .
(18) أجد حجم المجسّم الناتج من دوران المنطقة المظللة حول المحور .
(19) أجد حجم المجسّم الناتج من دوران المنطقة المحصورة بين منحنى الاقتران: في الفترة ، والمحور ، حول المحور .
(20) أجد حجم المجسّم الناتج من دوران المنطقة المحصورة بين منحنيي الاقترانين: حول المحور .
لكل يكون
(21) أجد حجم المجسم الناتج من دوران المنطقة المحصورة بين منحنى الاقتران: ، في الفترة والمستقيم حول المحور .
نلاحظ أن المنحنيين يقعان فوق المحور x وأن في الفترة








النقاشات