مسألة اليوم
مسألة اليوم
تطبيقات القيم القصوى
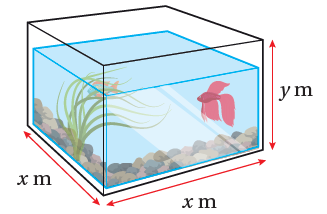 أرادت إسراء تصميم حوض أسماك زجاجي مفتوح من الأعلى، بحيث تكون سعته 0.2 m3 وأبعاده كما في الشكل المجاور. أجد أبعاد الحوض التي تجعل كميّة الزجاج المستعملة لصنعه أقل ما يمكن.
أرادت إسراء تصميم حوض أسماك زجاجي مفتوح من الأعلى، بحيث تكون سعته 0.2 m3 وأبعاده كما في الشكل المجاور. أجد أبعاد الحوض التي تجعل كميّة الزجاج المستعملة لصنعه أقل ما يمكن.
مساحة سطح الحوض المفتوح من الأعلى:
S = 4xy + x2
حجم الحوض: V = x2y
توجد قيمة حرجة واحدة هي:
إذن توجد قيمة صغرى محلية عندما:
وتكون أبعاد الحوض التي تجعل كمية الزجاج المستعملة لصنعه أقل ما يمكن هي:
إعداد : شبكة منهاجي التعليمية
10 / 07 / 2023
النقاشات