فكرة الدرس:
تعرُّفُ الاقترانِ العكسيِّ، وإيجادُهُ، وتحديدُ مجالِهِ ومداهُ.
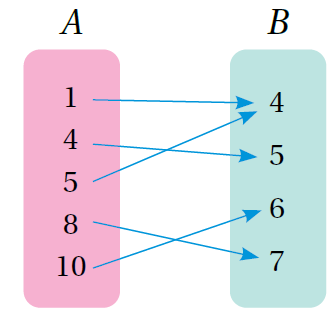
تعلَّمْتُ سابقًا أنَّ العلاقةَ تربطُ بينَ مجموعتيْنِ منَ العناصرِ، وأنَّ إحداهُما تُسمّى المجالَ، والأُخرى تُسمّى المدى. وبالنظرِ إلى العلاقةِ المُمثَّلةِ في المُخطَّطِ السهميِّ المجاورِ،
أُلاحِظُ أنَّ المجالَ هوَ: { 10 , 8 , 5 , 4 , A = {1 ، والمدى هوَ: .B = {4, 5, 6, 7}
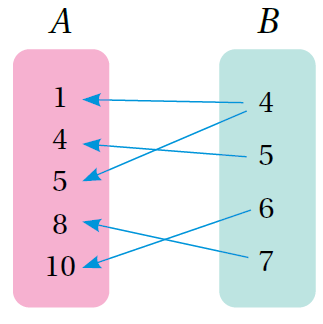
عندَ عكسِ اتجاهِ الأسهمِ لترتبطَ عناصرُ B بعناصرِ A تنتجُ علاقةٌ عكسيةٌ (inverse relation)، مجالُها B، ومداها A.
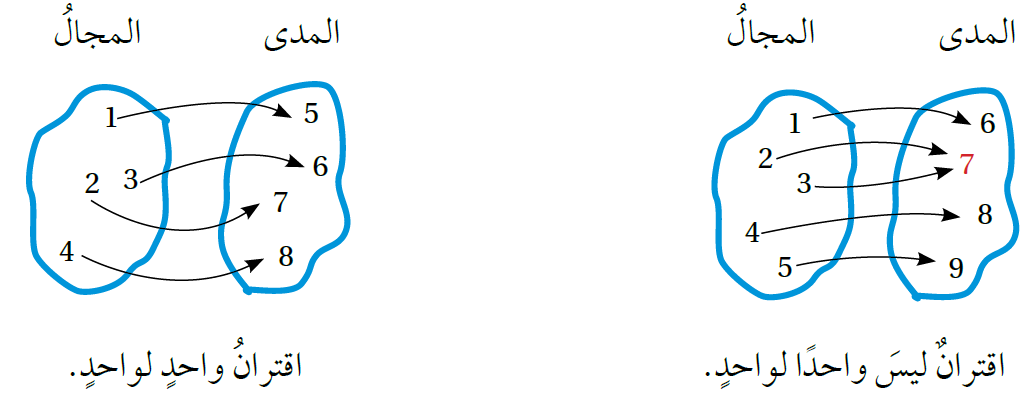
الاقتراناتُ هيَ نوعٌ خاصٌّ منَ العلاقاتِ؛ لأنَّ لها خاصيةً لا تُحقِّقُها جميعُ العلاقاتِ؛ فهيَ تربطُ كلَّ عنصرٍ في المجالِ بعنصرٍ واحدٍ فقطْ في المدى. وبما أنَّ كلَّ اقترانٍ هوَ علاقةٌ فإنَّهُ يُمكِنُ إيجادُ علاقةٍ عكسيةٍ للاقترانِ (معكوسُ الاقترانِ)، فإذا كانَ المعكوسُ اقترانًا أيضًا سُمِّيَّ اقترانًا عكسيًّا (inverse function). ويُرمَزُ إلى الاقترانِ العكسيِّ للاقترانِ (f(x بالرمزِ f-1(x)
يُمكِنُ تحديدُ إذا كانَ معكوسُ الاقترانِ f(x) يُمثِّلُ اقترانًا أمْ لا بالنظرِ إلىf(x) نفسِهِ؛ فإذا ارتبطَ كلُّ عنصرٍ في المدى بعنصرٍ واحدٍ فقطْ في المجالِ كانَ المعكوسُ اقترانًا، عندئذٍ يُسمّى f(x) اقترانَ واحدٍ لواحدٍ
يُمكِنُ أيضًا استعمالُ طريقةٍ تُسمّى اختبارَ الخطِّ الأفقيِّ (horizontal line test) ؛ للتحقُّقِ منْ أنَّ الاقترانَ هوَ واحدٌ لواحدٍ، وذلكَ برسمِ أيِّ خطٍّ أفقيٍّ، والتأكُّدِ أنَّهُ لا يقطعُ منحنى (f(x في أكثرَ منْ نقطةٍ.
إعداد : شبكة منهاجي التعليمية
24 / 04 / 2022
النقاشات