طباعة الدرس

أتدرب وأحل المسائل

تكامل اقترانات خاصة

أجد كلاً من التكاملات الآتية:

(1) $\int (e^{2x-3}-\sqrt{x}) dx$

$\int (e^{2x-3}-\sqrt{x}) dx=\int (e^{2x-3}-x^{1/2}) dx=\frac{1}{2}{e}^{2x-3}-\frac{2}{3}{x}^{3/2}+C$

(2) $\int (e^{0.5x}-\frac{3}{e^{0.5x}}) dx$

$\int (e^{0.5x}-\frac{3}{e^{0.5x}}) dx=\int (e^{0.5x}-3e^{-0.5x}) dx=2e^{0.5x}+6e^{-0.5x}+C$

(3) $\int (4\sin 5x-5\cos 4x) dx$

$\int (4\sin 5x-5\cos 4x) dx=-\frac{4}{5}\cos 5x-\frac{5}{4}\sin 4x+C$

(4) $\int (3\sec x \tan x-\frac{2}{5x}) dx$

$\int (3\sec x \tan x-\frac{2}{5x}) dx=3\sec x-\frac{2}{5}\ln \left|x\right|+C$

(5) $\int {(\sqrt{e^x}-\frac{1}{\sqrt{e^x}})}^2 dx$

$\begin{array}{rl}\int {(\sqrt{e^x}-\frac{1}{\sqrt{e^x}})}^2 dx& =\int (e^x-2+\frac{1}{e^x}) dx\\ & =\int (e^x-2+e^{-x}) dx\\ & =e^x-2x-e^{-x}+C\end{array}$

(6) $\int (\sin (5-3x)+2+4x^2) dx$

$\int (\sin (5-3x)+2+4x^2) dx=\frac{1}{3}\cos (5-3x)+2x+\frac{4}{3}{x}^3+C$

(7) $\int {(e^x+1)}^2 dx$

$\int {(e^x+1)}^2 dx=\int (e^{2x}+2e^x+1) dx=\frac{1}{2}{e}^{2x}+2e^x+x+C$

(8) $\int (e^{4-x}+\sin (4-x)+\cos (4-x\left)\right) dx$

$\begin{array}{rl}& \int (e^{4-x}+\sin (4-x)+\cos (4-x\left)\right)dx\\ & =-e^{4-x}+\cos (4-x)-\sin (4-x)+C\end{array}$

(9) $\int \frac{x^4-6}{2x} dx$

$\begin{array}{rl}\int \frac{x^2-6}{2x} dx& =\int (\frac{1}{2}x-\frac{3}{x}) dx\\ & =\frac{1}{4}{x}^2-3ln \left|x\right|+C\end{array}$

(10) $\int (3{\csc }^2 (3x+2)+\frac{5}{x}) dx$

$\int (3cs{c}^2 (3x+2)+\frac{5}{x}) dx=-cot (3x+2)+5ln \left|x\right|+C$

(11) $\int \frac{e^x+1}{e^x} dx$

$\int \frac{e^x+1}{e^x} dx=\int (1+e^{-x}) dx=x-e^{-x}+C$

(12) $\int \frac{e^x}{e^x+4} dx$

$\int \frac{e^x}{e^x+4} dx=ln |e^x+4|+C=ln (e^x+4)+C$

(13) $\int \frac{\cos 2x}{\sin x\cos x+4} dx$

$\begin{array}{rl}\int \frac{cos 2x}{sin xcos x+4} dx& =\int \frac{cos 2x}{\frac{1}{2}sin 2x+4} dx\\ & =ln |\frac{1}{2}sin 2x+4|+C=ln (\frac{1}{2}sin 2x+4)+C\end{array}$

(14) $\int \frac{dx}{5-\frac{x}{3}}$

$\begin{array}{rl}\int \frac{dx}{5-\frac{x}{3}}& =-3\int \frac{-\frac{1}{3}}{5-\frac{x}{3}} dx\\ & =-3ln |5-\frac{x}{3}|+C\end{array}$

(15) $\int \frac{1}{1-\sin x} dx$

$\begin{array}{rl}\int \frac{1}{1-sin x} dx& =\int \frac{1}{1-sin x}\times \frac{1+sin x}{1+sin x} dx\\ & =\int \frac{1+sin x}{1-si{n}^2 x} dx\\ & =\int \frac{1+sin x}{co{s}^2 x} dx\\ & =\int (se{c}^2 x+tan xsec x) dx\\ & =tan x+sec x+C\end{array}$

(16) $\int {\sec }^2 x(1+e^x{\cos }^2 x) dx$

$\begin{array}{rl}\int {\sec }^2 x(1+e^x{\cos }^2 x) dx& =\int ({\sec }^2 x+e^x) dx\\ & =\tan x+e^x+C\end{array}$

(17) $\int (\frac{2}{x}-2^x) dx$

$\int (\frac{2}{x}-2^x) dx=2\ln \left|x\right|-\frac{2^x}{\ln 2}+C$

(18) $\int \sin 3x \cos 2x dx$

$\begin{array}{rl}\int \sin 3x\cos 2x dx& =\frac{1}{2}\int (\sin 5x+\sin x) dx\\ & =-\frac{1}{10}\cos 5x-\frac{1}{2}\cos x+C\end{array}$

 $\int \frac{2x+3}{3x^2+9x-1}dx$ (19)

$\begin{array}{rl}\int \frac{2x+3}{3x^2+9x-1}dx& =\frac{1}{3}\int \frac{6x+9}{3x^2+9x-1}dx\\ & =\frac{1}{3}\ln |3x^2+9x-1|+C\end{array}$

$\int \frac{x^2+x+1}{x^2+1}dx$ (20)

$\begin{array}{rl}\int \frac{x^2+x+1}{x^2+1}dx& =\int (\frac{x^2+1}{x^2+1}+\frac{x}{x^2+1})dx\\ & =\int (1+\frac{1}{2}\times \frac{2x}{x^2+1})dx\\ & =x+\frac{1}{2}\ln (x^2+1)+C\end{array}$

$\int (\frac{1+\cos x}{{\sin }^{2}x}+({\sin }^{2}x\csc x))dx$ (21)

$\begin{array}{rl}\int (\frac{1+\cos x}{{\sin }^{2}x}+{\sin }^{2}x\csc x)dx& =\int ({\csc }^{2}x+\cot x\csc x+\sin x)dx\\ & =-\cot x-\csc x-\cos x+C\end{array}$

$\int (\sec x+\tan x{)}^{2}dx$ (22)

$\begin{array}{rl}\int (\sec x+\tan x{)}^{2}dx& =\int ({\sec }^{2}x+2\sec x\tan x+{\tan }^{2}x)dx\\ & =\int ({\sec }^{2}x+2\sec x\tan x+{\sec }^{2}x-1)dx\\ & =\int (2{\sec }^{2}x+2\sec x\tan x-1)dx\\ & =2\tan x+2\sec x-x+C\end{array}$

$\int \frac{e^x-e^{-x}}{e^x+e^{-x}}dx$ (23)

$\int \frac{e^x-e^{-x}}{e^x+e^{-x}}dx=\ln (e^x+e^{-x})+C$

$\int \frac{x^2}{x^3-3}dx$ (24)

$\int \frac{x^2}{x^3-3}dx=\frac{1}{3}\int \frac{3x^2}{x^3-3}dx=\frac{1}{3}\ln |x^3-3|+C$

$\int (9{\cos }^{2}x-{\sin }^{2}x-6\sin x\cos x)dx$ (25)

$\begin{array}{rl}& \int (9{\cos }^{2}x-{\sin }^{2}x-6\sin x\cos x)dx\\ & =\int (9{\cos }^{2}x-(1-{\cos }^{2}x)-6\sin x\cos x)dx\\ & =\int (10{\cos }^{2}x-1-6\sin x\cos x)dx\\ & =\int (10\left(\frac{1+\cos 2x}{2}\right)-1-3\sin 2x)dx\\ & =\int (5+5\cos 2x-1-3\sin 2x)dx=\int (4+5\cos 2x-3\sin 2x)dx\\ & =4x+\frac{5}{2}\sin 2x+\frac{3}{2}\cos 2x+C\end{array}$

$\int ({\cos }^{4}x-{\sin }^{4}x)dx$ (26)

$\begin{array}{rl}\int ({\cos }^{4}x-{\sin }^{4}x)dx& =\int ({\cos }^{2}x-{\sin }^{2}x)({\cos }^{2}x+{\sin }^{2}x)dx\\ & =\int ({\cos }^{2}x-{\sin }^{2}x)dx\\ & =\int \cos 2xdx\\ & =\frac{1}{2}\sin 2x+C\end{array}$

أجد قيمة كل من التكاملات الآتية:

${\int }_0^{\pi }2\cos \frac{1}{2}xdx{\int }_0^{\pi }2\cos \frac{1}{2}xdx$ (27)

${\int }_0^{\pi }2\cos \frac{1}{2}xdx={4\sin \frac{1}{2}x|}_0^{\pi }=4(\sin \frac{\pi }{2}-\sin 0)=4$

${\int }_0^{2\pi }|\sin x|dx$ (28)

$\begin{array}{rl}& |sinx|=\{\begin{array}{rl}sinx& ,0\le x\le \pi \\ -sinx& ,\pi <x\le 2\pi \end{array}\\ & {\int }_0^{2\pi }|sinx|dx={\int }_0^{\pi }sinxdx+{\int }_{\pi }^{2\pi }-sinxdx\\ & =-{cosx|}_0^{\pi }+{cosx|}_{\pi }^{2\pi }\\ & =-(cos\pi -cos0)+cos2\pi -cos\pi \\ & =-(-2)+1-(-1)=4\end{array}$

${\int }_{\pi /6}^{\pi /3}3{\tan }^{2}xdx$ (29)

$\begin{array}{rl}{\int }_{\frac{\pi }{6}}^{\frac{\pi }{3}}3{\tan }^{2}xdx& ={\int }_{\frac{\pi }{6}}^{\frac{\pi }{3}}3({\sec }^{2}x-1)dx\\ & ={3(\tan x-x)|}_{\frac{\pi }{6}}^{\frac{\pi }{3}}\\ & =3(\tan \frac{\pi }{3}-\frac{\pi }{3})-3(\tan \frac{\pi }{6}-\frac{\pi }{6})\\ & =2\sqrt{3}-\frac{\pi }{2}\end{array}$

${\int }_1^e\frac{8x}{x^2+1}dx$ (30)

$\begin{array}{rl}{\int }_1^e\frac{8x}{x^2+1}dx& =4{\int }_1^e\frac{2x}{x^2+1}dx\\ & ={4\ln |x^2+1||}_1^e\\ & =4\ln (e^2+1)-4\ln 2\\ & =4\ln \left(\frac{e^2+1}{2}\right)\end{array}$

${\int }_0^{\pi /6}\sin 3x\cos xdx$(31)

$\begin{array}{rl}{\int }_0^{\frac{\pi }{6}}\sin 3x\cos xdx& =\frac{1}{2}{\int }_0^{\frac{\pi }{6}}(\sin 4x+\sin 2x)dx\\ & ={(-\frac{1}{8}\cos 4x-\frac{1}{4}\cos 2x)|}_0^{\frac{\pi }{6}}\\ & =-\frac{1}{8}\cos \frac{4\pi }{6}-\frac{1}{4}\cos \frac{2\pi }{6}-(-\frac{1}{8}\cos 0-\frac{1}{4}\cos 0)\\ & =\frac{5}{16}\end{array}$

${\int }_{\pi /4}^{\pi /3}\frac{{\cot }^{2}x}{1+{\cot }^{2}x}dx$ (32)

$\begin{array}{rl}{\int }_{\frac{\pi }{4}}^{\frac{\pi }{3}}\frac{{\cot }^{2}x}{1+{\cot }^{2}x}dx& ={\int }_{\frac{\pi }{4}}^{\frac{\pi }{3}}\frac{{\cot }^{2}x}{{\csc }^{2}x}dx\\ & ={\int }_{\frac{\pi }{4}}^{\frac{\pi }{3}}\frac{{\cos }^{2}x}{{\sin }^2{\csc }^{2}x}dx\\ & ={\int }_{\frac{\pi }{4}}^{\frac{\pi }{3}}\frac{{\cos }^{2}x}{{\sin }^{2}x\left(\frac{1}{{\sin }^{2}x}\right)}dx\\ & ={\int }_{\frac{\pi }{4}}^{\frac{\pi }{3}}{\cos }^{2}xdx\\ & =\frac{1}{2}{\int }_{\frac{\pi }{4}}^{\frac{\pi }{3}}(1+\cos 2x)dx\\ & ={\frac{1}{2}(x+\frac{1}{2}\sin 2x)|}_{\frac{\pi }{4}}^{\frac{\pi }{3}}\\ & =\frac{\pi }{6}+\frac{1}{4}\sin \frac{2\pi }{3}-(\frac{\pi }{8}+\frac{1}{4}\sin \frac{2\pi }{4})\end{array}$

${\int }_0^3(x-5^x)dx$ (33)

$\begin{array}{rl}{\int }_0^3(x-5^x)dx& ={(\frac{1}{2}{x}^2-\frac{5^x}{\ln 5})|}_0^3\\ & =\frac{9}{2}-\frac{125}{\ln 5}-(0-\frac{1}{\ln 5})=\frac{9}{2}-\frac{124}{\ln 5}\end{array}$

${\int }_0^4|x^2-4x+3|dx$ (34)

$\begin{array}{rl}& |x^2-4x+3|=\{\begin{array}{cc}{x}^2-4x+3& ,x<1\\ -x^2+4x-3,1\le x\le 3& \\ x^2-4x+3& ,x>3\end{array}\\ & {\int }_0^4|x^2-4x+3|dx\\ & ={\int }_0^1(x^2-4x+3)dx+{\int }_1^3(-x^2+4x-3)dx+{\int }_3^4(x^2-4x+3)dx\\ & ={(\frac{1}{3}{x}^3-2x^2+3x)|}_0^1+{(-\frac{1}{3}{x}^3+2x^2-3x)|}_1^3+{(\frac{1}{3}{x}^3-2x^2+3x)|}_3^4\\ & =\frac{1}{3}-2+3-0+(-9+18-9)-(-\frac{1}{3}+2-3)+\frac{64}{3}-32+12\end{array}$

${\int }_1^4(3-|x-3\left|\right)dx$ (35)

$\begin{array}{rl}& |x-3|=\{\begin{array}{ll}3-x& ,x\le 3\\ x-3& ,x>3\end{array}\\ & {\int }_1^4(3-|x-3\left|\right)dx={\int }_1^3(3-(3-x\left)\right)dx+{\int }_3^4(3-(x-3\left)\right)dx\\ & ={\int }_1^{3}xdx+{\int }_3^4(6-x)dx\\ & ={\frac{1}{2}{x}^2|}_1^3+{(6x-\frac{1}{2}{x}^2)|}_3^4\\ & =\frac{9}{2}-\frac{1}{2}+24-8-(18-\frac{9}{2})\\ & =\frac{13}{2}\end{array}$

(36) إذا كان $f\left(x\right)=\{\begin{array}{ll}{x}^2+4& ,x<0\\ 4-x& ,x\ge 0\end{array}$، فأجد قيمة: ${\int }_{-1}^{1}f\left(x\right)dx$.

$\begin{array}{rl}{\int }_{-1}^{1}f\left(x\right)dx& ={\int }_{-1}^0(x^2+4)dx+{\int }_0^1(4-x)dx\\ & ={(\frac{1}{3}{x}^3+4x)|}_{-1}^0+{(4x-\frac{1}{2}{x}^2)|}_0^1\\ & =0-(-\frac{1}{3}-4)+4-\frac{1}{2}-0\\ & =\frac{47}{6}\end{array}$

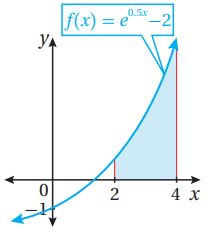(37) أجد مساحة المنطقة المظللة بين المحور x ومنحنى الاقتران: $f\left(x\right)=e^{0.5x}-2$ الممثل في الشكل المجاور.

$\begin{array}{rl}A={\int }_2^4(e^{0.5x}-2)dx& ={(2e^{0.5x}-2x)|}_2^4\\ & =2e^2-8-(2e-4)\\ & =2e^2-2e-4\end{array}$

(38) إذا كان: ${\int }_a^{3a}\frac{2x+1}{x}dx=\ln 12$، فأجد قيمة الثابت a، حيث: $a>0$.

$\begin{array}{rl}& {\int }_a^{3a}\frac{2x+1}{x}dx={\int }_a^{3a}2+\frac{1}{x}dx\\ & ={(2x+\ln |x\left|\right)|}_a^{3a}\\ & =6a+\ln 3a-2a-\ln a\\ & =4a+\ln 3\\ & \Rightarrow 4a+\ln 3=\ln 12\\ & \Rightarrow 4a=\ln 12-\ln 3\\ & 4a=\ln \frac{12}{3}\\ & \Rightarrow a=\frac{1}{4}\ln 4\end{array}$

(39) أثبت أن: ${\int }_0^a\frac{x}{x^2+a^2}dx=\ln \sqrt{2}$، حيث: $a\ne 0$.

$\begin{array}{rl}{\int }_0^a\frac{x}{x^2+a^2}dx& =\frac{1}{2}{\int }_0^a\frac{2x}{x^2+a^2}dx\\ & ={\frac{1}{2}\ln (x^2+a^2)|}_0^a\\ & =\frac{1}{2}(\ln \left(2a^2\right)-\ln \left(a^2\right))=\frac{1}{2}\ln 2=\ln \sqrt{2}\end{array}$

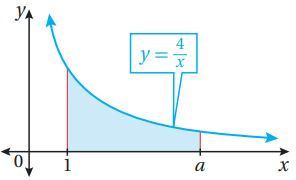(40) يبين الشكل المجاور منحنى الاقتران: $f\left(x\right)=\frac{4}{x}$. إذا كانت مساحة المنطقة المحصورة بين منحنى الاقتران $f\left(x\right)$، والمحور x، والمستقيمين: $x=a،x=1$، هي 10 وحدات مربعة، فأجد قيمة الثابت a.

$\begin{array}{rl}& A={\int }_1^a\frac{4}{x}dx={4\ln \left|x\right||}_1^a=4\ln a-4\ln 1=4\ln a\\ & \Rightarrow 4\ln a=10\Rightarrow \ln a=\frac{5}{3}\Rightarrow a=e^{\frac{5}{2}}\end{array}$

(41) إذا كان: $f\left(x\right)=\int \cos (\frac{1}{2}x+\pi )dx$، وكان: $f\left(\pi \right)=3$، فأجد $f\left(0\right)$.

$\begin{array}{rl}& f\left(x\right)=\int \cos (\frac{1}{2}x+\pi )dx=2\sin (\frac{1}{2}x+\pi )+C\\ & f\left(\pi \right)=2\sin (\frac{1}{2}\pi +\pi )+C\\ & 3=2\sin \frac{3\pi }{2}+C\\ & 3=-2+C\Rightarrow C=5\\ & \Rightarrow f\left(x\right)=2\sin (\frac{1}{2}x+\pi )+5\\ & \Rightarrow f\left(0\right)=2\sin \pi +5=5\end{array}$

(42) إذا كان: $y=\int \sin (\frac{\pi }{2}-2x)dx$، وكان: 1=y عندما $x=\frac{\pi }{4}$، فأثبت أنه يمكن كتابة y في صورة: $y=\frac{1+\sin 2x}{2}$.

$\begin{array}{rl}& y=\int \sin (\frac{\pi }{2}-2x)dx=\frac{-\cos (\frac{\pi }{2}-2x)}{-2}+C=\frac{1}{2}\cos (\frac{\pi }{2}-2x)+C\\ & {y|}_{x=\frac{\pi }{4}}=\frac{1}{2}\cos (\frac{\pi }{2}-\frac{\pi }{2})+C\\ & 1=\frac{1}{2}+C\Rightarrow C=\frac{1}{2}\\ & \Rightarrow y=\frac{1}{2}\cos (\frac{\pi }{2}-2x)+\frac{1}{2}\\ & \Rightarrow y=\frac{1}{2}\sin 2x+\frac{1}{2}\\ & \Rightarrow y=\frac{1+\sin 2x}{2}\end{array}$

(43) يمثل الاقتران: $\frac{dy}{dx}=e^{2x}-2e^{-x}$ ميل المماس لمنحنى الاقتران y. أجد قاعدة الاقتران y إذا علمت أن منحناه يمر بالنقطة (0,1).

$\begin{array}{rl}& y=\int (e^{2x}-2e^{-x})dx=\frac{1}{2}{e}^{2x}+2e^{-x}+C\\ & {y|}_{x=0}=\frac{1}{2}+2+C\\ & 1=\frac{5}{2}+C\Rightarrow C=-\frac{3}{2}\\ & \Rightarrow y=\frac{1}{2}{e}^{2x}+2e^{-x}-\frac{3}{2}\end{array}$

(44) إذا كان: ${\int }_{\pi /9}^{\pi }(9+\sin 3x)dx=a\pi +b$، فأجد قيمة الثابتين النسبيين: a وb.

$\begin{array}{rl}& {\int }_{\frac{\pi }{9}}^{\pi }(9+\sin 3x)dx={(9x-\frac{1}{3}\cos 3x)|}_{\frac{\pi }{9}}^{\pi }\\ & =9\pi -\frac{1}{3}\cos 3\pi -\pi +\frac{1}{3}\cos \frac{\pi }{3}\\ & =8\pi +\frac{1}{3}+\frac{1}{6}\\ & =8\pi +\frac{1}{2}\\ & \Rightarrow 8\pi +\frac{1}{2}=a\pi +b\end{array}$

ونظراً لأن a وb نسبيان، فلا يوجد حل لهذه المعادلة سوى أن يكون: $a=8,b=\frac{1}{2}$

(45) يمثل الاقتران: $f^{\mathrm{\prime }}\left(x\right)={\cos }^{2}x$ ميل المماس لمنحنى الاقتران $f\left(x\right)$. أجد قاعدة الاقتران f إذا علمت أن يمر بنقطة الأصل.

$\begin{array}{rl}f\left(x\right)& =\int {\cos }^{2}xdx=\frac{1}{2}\int (1+\cos 2x)dx=\frac{1}{2}(x+\frac{1}{2}\sin 2x)+C\\ f\left(0\right)& =\frac{1}{2}(0+\frac{1}{2}\sin 0)+C\\ 0& =0+C\Rightarrow C=0\\ f\left(x\right)& =\frac{1}{2}x+\frac{1}{4}\sin 2x\end{array}$

يتحرك جسيم في مسار مستقيم، وتعطى سرعته المتجهة بالاقتران: $\mathit{v}\mathbf{\left(}\mathit{t}\mathbf{\right)}\mathbf{=}{\mathit{e}}^{\mathbf{-}\mathbf{2}\mathbf{t}}$، حيث t الزمن بالثواني، وv سرعته المتجهة بالمتر لكل ثانية. إذا كان الموقع الابتدائي للجسيم هو 3m، فأجد كلاً مما يأتي:

(46) موقع الجسيم بعد t ثانية.

$\begin{array}{rl}s\left(t\right)& =\int e^{-2t}dt=-\frac{1}{2}{e}^{-2t}+C\\ s\left(0\right)& =-\frac{1}{2}+C=3\Rightarrow C=\frac{7}{2}\\ 3& =-\frac{1}{2}+C\Rightarrow C=\frac{7}{2}\\ s\left(t\right)& =-\frac{1}{2}{e}^{-2t}+\frac{7}{2}\end{array}$

(47) موقع الجسيم بعد 100 ثانية.

$s\left(100\right)=-\frac{1}{2}{\mathrm{e}}^{-200}+\frac{7}{2}\approx 3.5m$

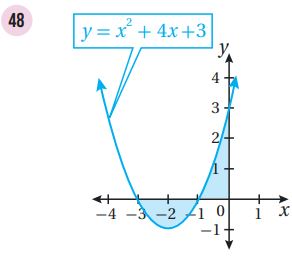بيئة: في دراسة تناولت أحد أنواع الحيوانات المهددة بالانقراض في غابة، تبين أن عدد حيوانات هذا النوع (t)P يتغير بمعدل: ${\mathit{P}}^{\mathbf{\prime }}\mathbf{\left(}\mathit{t}\mathbf{\right)}\mathbf{=}\mathbf{-}\mathbf{0}\mathbf{.}\mathbf{51}{\mathit{e}}^{\mathbf{-}\mathbf{0}\mathbf{.}\mathbf{03}\mathbf{t}}$، حيث t الزمن بالسنوات بعد بدء الدراسة:

(48) أجد قاعدة الاقتران (t)P عند أي زمن t، علما بأن عدد حيوانات هذا النوع عند بدء الدراسة هو 500 حيوان.

$\begin{array}{rl}& P\left(t\right)=\int -0.51{\mathrm{e}}^{-0.03t}dt=\frac{-0.51}{-0.03}{\mathrm{e}}^{-0.03t}+C=17{\mathrm{e}}^{-0.03t}+C\\ & P\left(0\right)=17+C\\ & 500=17+C\Rightarrow C=483\\ & P\left(t\right)=17{\mathrm{e}}^{-0.03t}+483\end{array}$

(49) أجد عدد الحيوانات بعد 10 سنوات من بدء الدراسة، مقرباً إجابتي إلى أقرب عدد صحيح.

$P\left(10\right)=17{\mathrm{e}}^{-0.3}+483\approx 496$

طب: في تجربة لدواء جديد أعطي لمريض لديه ورم حميد، حجمه $\mathbf{\text{30}}{\mathbf{cm}}^{\mathbf{3}}$، تبين أن حجم الورم بعد t يوماً من بدء التجربة يتغير بمعدل: ${\mathit{P}}^{\mathbf{\prime }}\mathbf{\left(}\mathit{t}\mathbf{\right)}\mathbf{=}\mathbf{0}\mathbf{.}\mathbf{15}\mathbf{-}\mathbf{0}\mathbf{.}\mathbf{9}{\mathit{e}}^{\mathbf{0}\mathbf{.}\mathbf{006}\mathbf{t}}$ مقيساً بوحدة $\mathbf{(}{\mathbf{cm}}^{\mathbf{3}}\mathbf{/}\mathbf{\text{day}}\mathbf{)}$:

(50) أجد قاعدة حجم الورم بعد t يوماً من بدء التجرية.

$\begin{array}{rl}& P\left(t\right)=\int (0.15-0.9{\mathrm{e}}^{0.006t})dt\\ & =0.15t-\frac{0.9}{0.006}{e}^{0.006t}+C\\ & =0.15t-150{\mathrm{e}}^{0.006t}+C\\ & P\left(0\right)=-150+C\\ & 30=-150+C\Rightarrow C=180\\ & P\left(t\right)=0.15t-150{\mathrm{e}}^{0.006t}+180\end{array}$

(51) أجد حجم الورم بعد 10 أيام من بدء التجربة.

$P\left(10\right)=1.5-150{\mathrm{e}}^{0.06}+180\approx 22.2{\mathrm{cm}}^3$