 |
اختبار نهاية الوحدة
المتجهات
أختار رمز الإجابة الصحيحة في كل مما يأتي:
(1) إذا كانت ، فإن الصورة الإحداثية للمتجه هي:
(a
(b
(c
(d
(2) إذا كان: ، وكان: ، فإن c تساوي:
4 (a
3,5- (b
15 (c
4,4- (d
(3) إذا كان PQR مستقيماً، حيث: ، فإن التعبير عن المتجه بدلالة هو:
(a
(b
(c
(d
(4) النقطة الواقعة على المستقيم الذي له المعادلة المتجهة: ، والإحداثـي y لها 10 هي:
(a
(b
(c
(d
(5) إذا كان: ، وكان: ، فإن يساوي:
(a
(b
(c
(d
(6) إذا كان قياس الزاوية بيـن هو ، وكان: ، وكان: ، فإن مقدار هو:
3 (a
5 (b
6 (c
24 (d
(7) إذا كان: ، وكان: ، وكان: فإن قيمة a هي:
10- (a
5- (b
1- (c
5 (d
(8) إذا كان المتجه ، والمتجه: متعامدين، فإن قيمة q هي:
0 (a
8 (b
10 (c
18 (d
(10) إذا وقعت النقاط: على مستقيم واحد، فما قيمة كل من h وk؟
E,F,G تقع على استقامة واحدة، إذن ، ومنه:
إذن، يوجد عدد حقيقي مثل c بحيث:
(11) إذا كانت ، وكانت النقطة D تقع على المستقيم المار بالنقطة A والنقطة B، وكانت الزاوية CDA قائمة، فأجد إحداثيات النقطة D.
إذا كانت: معادلة متجهة للمستقيم ، وكانت: معادلة متجهة للمستقيم ، فأجيب عن السؤالين الأتبين تباعاً:
(12) أجد إحداثيات نقطة تقاطع المستقيمين: .
لإيجاد نقطة التقاطع نساوي في المعادلتين ونساوي إحداثياتهما المتناظرة لنجد قيمة الوسيطين :
وهاتان القيمتان تحققان المعادلة الثالثة الآتية:
نجد نقطة تقاطعهما بتعويض في معادلة ، وهي النقطة
(13) أجد قياس الزاوية الحادة بين المستقيمين:.
اتجاه المستقيم :
اتجاه المستقيم :
لتكن قياس الزاوية بين إذن:
فيكون قياس الزاوية الحادة بين هو حيث:
إذا كانت ، فأجيب عن الأسئلة الأربعة الآتية تباعاً:
(14) أكتب معادلة متجهة للمستقيم .
(15) أكتب معادلة متجهة للمستقيم .
(16) إذا كان قياس ، فأثبت أن: .
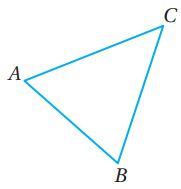
(17) أجد مساحة المثلث ABC.
(18) إذا كانت: معادلة متجهة للمستقيم l، وكانت النقطة V تقع على المستقيم l، حيث: فما إحداثيات النقطة V؟
V نقطة على l إذن يكون متجه موقعها:
اتجاه l هو:
وبما أن إذن يكون: ومنه:
يمر المستقيم بالنقطتين: E وF، ويمر المستقيم بالنقطتين: G وH. أحدد إذا كان هذان المستقيمان متوازيين أو متخالفين أو متقاطعين، ثم أجد إحداثيات نقطة التقاطع إذا كانا متقاطعين في كل مما يأتي:
(19)
نلاحظ أنه لا يوجد عدد حقيقي k يحقق كون النسب بين الإحداثيات المتناظرة غير متساوية، فالمستقيمان غير متوازيين:
معادلة هي:
معادلة هي:
نساوي في المعادلتين ونساوي إحداثياتهما المتناظرة لنجد قيم t,u لمعرفة نقطة التقاطع:
هذه القيم لا تحقق المعادلة (2)، إذن المستقيمان ليسا متقاطعين ولا متوازيين، فهما متخالفان.
(20)
بما أن النسب بين الإحداثيات المتناظرة غير ثابتة، فإنه لا يوجد عدد حقيقي k حيث وهذا يعني أن المستقيمين غير متوازيين.
بتبسيط اتجاه بقسمته على 5 تكون معادلته:
بتبسيط اتجاه بقسمته على 6 تكون معادلته:
نساوي في المعادلتين ونساوي إحداثياتهما المتناظرة لنجد قيم t,u لمعرفة نقطة التقاطع:
لكن هذه القيم لا تحقق المعادلة (2)، إذن المستقيمان ليسا متقاطعين ولا متوازيين، فهما متخالفان.
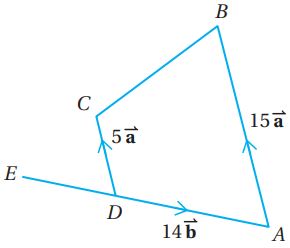
وهذا يعني أن
لكن المتجهين ينطلقان من النقطة E نفسها، إذن النقاط الثلاثة B,C,E تقع على استقامة واحدة.