طباعة الدرس

أتحقق من فهمي

المعدلات المرتبطة

معدل تغير المساحة والحجم بالنسبة إلى الزمن

أتحقق من فهمي صفحة 78

تنفخ ماجدة بالوناً على شكل كرة، فيزداد حجمه بمعدل 80 cm³/s . أجد مُعدّل زيادة نصف قطر البالون عندما يكون نصف القطر 6 cm .

ليكن حجم الكرة V ، وطول نصف قطرها  r

 $\frac{dv}{dt}$ = 80 cm³/s

معدل التغير المعطي:

${\overline{)\frac{dr}{dt}}}_{ r=6}$

معدل التغير المطلوب:

V = $\frac{4}{3}$πr³

حجم البالون الكروي:

$\frac{dv}{dt}$ = 4πr² $\frac{dr}{dt}$

 

${\overline{)\frac{dv}{dt}}}_{ r=6}$ = 4π(6)² ${\overline{)\frac{dr}{dt}}}_{ r=6}$

80 = 144π ${\overline{)\frac{dr}{dt}}}_{ r=6}$

${\overline{)\frac{dr}{dt}}}_{ r=6}$ = $\frac{80}{144\mathrm{\pi }}$

 = $\frac{5}{9\mathrm{\pi }}$ cm/s

---

معدل تغير المسافة بالنسبة إلى الزمن

أتحقق من فهمي صفحة 80

تحركت السيارة A والسيارة B في الوقت نفسه، ومن النقطة نفسها، بحيث اتجهت السيارة A نحو الشمال بسرعة 45 km/h ، واتجهت السيارة B نحو الشرق بسرعة 40 km/h . أجد مُعدّل تغير البعد بين السيارتين بعد ساعتين من انطلاقهما.

ليكن بعد A عن نقطة الانطلاق يساوي x ، وبعد B عن نقطة الانطلاق يساوي y ، والبعد بين A ، و B يساوي z

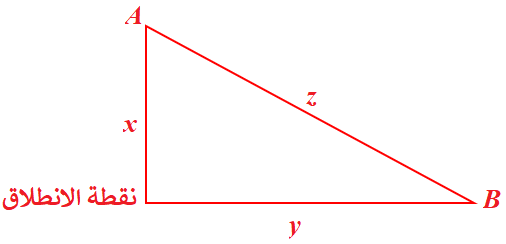
معدل التغير المعطى:

$\frac{dx}{dt}$ = 45 km/h , $\frac{dy}{dt}$ = 40 km/h

معدل التغير المطلوب:

${\overline{)\frac{dz}{dt}}}_{ t=2}$

بعد ساعتين من الحركة يكون:

x = 45 x 2 = 90 km  ,  y = 40 x 2 = 80 km

من نظرية فيثاغورس:

z² = x² + y²

^{z = $\sqrt{x^2 + y^2}$}

$\frac{dz}{dt}$ = $\frac{x{\displaystyle \frac{dx}{dt}} + y\frac{dy}{dt}}{\sqrt{x^2 + y^2}}$

${\overline{)\frac{dz}{dt}}}_{ t=2}$ = $\frac{x{\displaystyle \frac{dx}{dt}} + y\frac{dy}{dt}}{\sqrt{x^2 + y^2}}$

             = $\frac{90 \mathrm{x} 45 + 80 \mathrm{x} 40}{\sqrt{8100 + 6400}}$ = $\frac{7250}{10 \sqrt{145}}$ = $\frac{725}{\sqrt{145}}$ $\approx$ 60.21 km/h

---

معدل تغير الزاوية بالنسبة إلى الزمن

أتحقق من فهمي صفحة 82

أمسك ولد ببكرة خيط طائرة ورقية تحلق على ارتفاع 50 m فوق سطح الأرض، وتتحرك أفقياً بسرعة 2 m/s . أجد معدّل تغير الزاوية بين الخيط والمستوى الأفقي عندما يكون طول الخيط 100 m ، علماً بأن ارتفاع يد الولد عن الأرض 1.5 m

ليكن طول الخيط L وقياس الزاوية بي الخيط الأفقي Ɵ ، وبعد الطائرة أفقياً هو x .

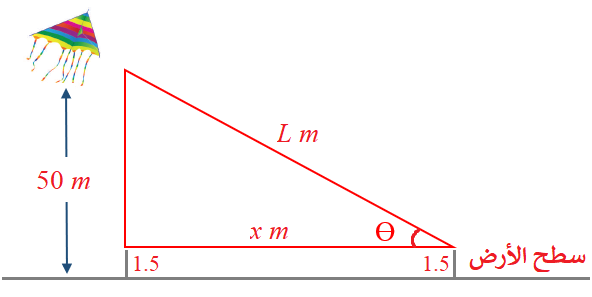
المعطى:

 $\frac{dx}{dt}$ = 2 m/s

المطلوب:

${\overline{)\frac{d\theta }{dt}}}_{ L=100}$ 

tan Ɵ = $\frac{50 - 1.5}{x}$ =  $\frac{48.5}{x}$

sec² Ɵ $\frac{d\theta }{dt}$ = - $\frac{48.5 {\displaystyle \frac{dx}{dt}}}{x^2}$

$\frac{L^2}{x^2}$ x $\frac{d\theta }{dt}$ = $\frac{48.5 {\displaystyle \frac{dx}{dt}}}{x^2}$

$\frac{d\theta }{dt}$ = $\frac{48.5 ({\displaystyle \frac{dx}{dt})}}{x^2}$ x $\frac{x^2}{L^2}$ = $\frac{48.5 {\displaystyle \left(\frac{dx}{dt}\right)}}{L^2}$

${\overline{)\frac{d\theta }{dt}}}_{ L=100}$ = $\frac{48.5 \left(2\right)}{{\left(100\right)}^2}$ ≈ -0.0097 rad/s

---

معدل التغير بالنسبة إلى الزمن والحركة الدائرية

أتحقق من فهمي صفحة 84

أنشئت منارة على جزيرة صغيرة، بحيث كانت على مستوى سطح البحر، وهي تبعد مسافة 3 km عن أقرب نقطة على ساحل مستقيم. إذا كان مصباح المنارة يُكمل 4 دورات في الدقيقة، فأجد سرعة تحرّك بقعة الضوء على خط الساحل عندما تبعد مسافة 1 km عن أقرب نقطة إلى المنارة.

لتكن الأبعاد كما في الشكل أدناه:

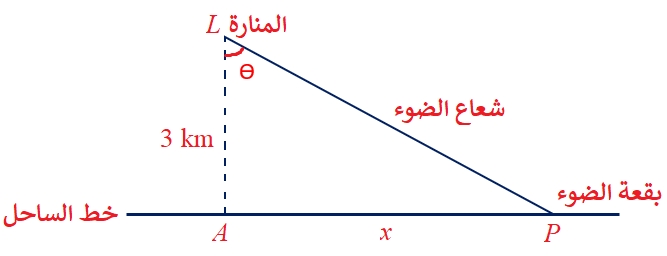
المعطى:

$\omega$ = $\frac{d\theta }{dt}$ = 4(2π) = 8π rad/min

المطلوب:

${\overline{)\frac{dx}{dt}}}_{ x=1}$

tan Ɵ = $\frac{x}{3}$

sec² Ɵ $\frac{d\theta }{dt}$ = $\frac{1}{3}$$\frac{dx}{dt}$

$\frac{x^2 + 9}{3}$ x $\frac{d\theta }{dt}$ = $\frac{1}{3}$$\frac{dx}{dt}$

$\frac{dx}{dt}$ = (x² + 9) $\frac{d\theta }{dt}$

 ${\overline{)\frac{dx}{dt}}}_{ x=1}$ = (1 + 9) (8π) = 80π km/min

سرعة بقعة الضوء على الساحل 80π km/min عندما تبعد 1 km عن A .

---