أتحقق من فهمي

النهايات والاتصال

إيجاد النهايات بيانياً وعدديًا

أتحقق من فهمي صفحة (54):

أجد كلاً من النهايات الآتية بيانياً وعدديًا:

(a)

الحل بيانياً:

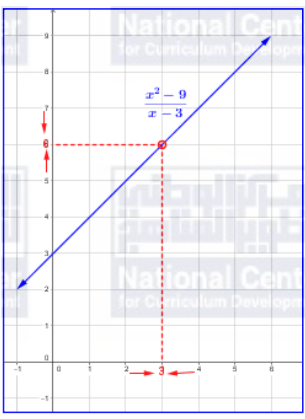
الحل عددياً:

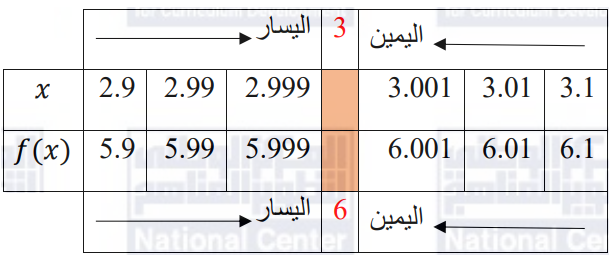
(b)

الحل بيانياً:

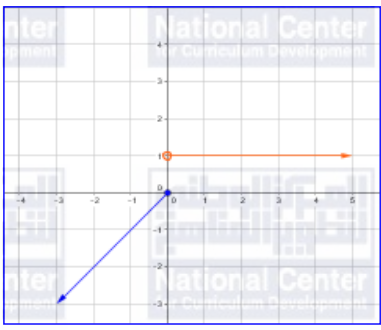
الحل عددياً:

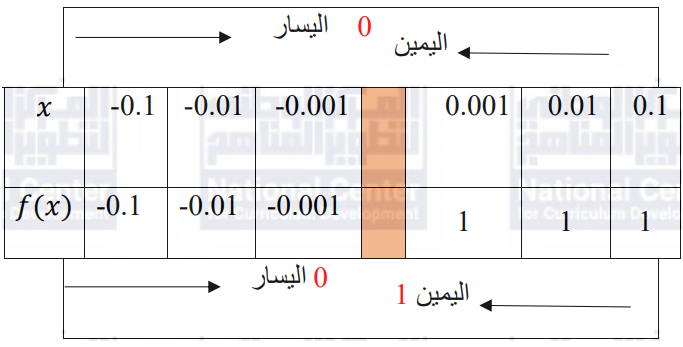
نهايات تتضمن (المالانهاية)

أتحقق من فهمي صفحة (56):

أجد كلاً من النهايات الآتية بيانياً:

(a)

غير موجودة.

(b) =

إيجاد النهايات جبرياً

أتحقق من فهمي صفحة (58):

أستعمل خصائص النهايات لحساب كل نهاية مما يأتي:

(a)

(b)

=

  =

  =

أتحقق من فهمي صفحة (59):

أجد كل نهاية ممّا يأتي باستعمال التعويض المباشر إذا كان ممكناً، وإلا فأذكر السبب:

(a)

= 3(2)² – 5(2) + 4 = 6

(b)

العدد (1) لا يقع ضمن مجال الاقتران فلذلك لا يمكن إيجاد النهاية بالتعويض المباشر.

(c)

=

(d)

= = 8

غير موجودة.

أتحقق من فهمي صفحة (61):

أجد كلّ نهاية ممّا يأتي:

(a)

 = =  = 7

(b)

 = x

=  =  =   = 

(c)

= 1

= -1

الاتصال

أتحقق من فهمي صفحة (64):

أحدّد إذا كان كلّ اقتران ممّا يأتي متصلاً عند قيمة x المعطاة، مبرراً إجابتي:

(a)

الاقتران متصل عند x = 1 ؛ لأن

(b)

الاقتران غير متصل عند x = 5 ؛ لأن الاقتران غير معرف عند x = 5

(c)

h(3) = 5 – 3 = 3

h(3) == 2

إذن الاقتران متصل عند x = 3

(d)

p(5) = 10

              =

 p(5) =

إذن الاقتران متصل عند x = 5