أتدرب وأحل المسائل
حل معادلات القيمة المطلقة ومتبايناتها
أجد قيمة كل من المقادير الجبرية الآتية عند القيمة المعطاة:
1) |5x + 2| + 1, x = -3
14
2) |14 - x| - 18, x = 1
-5
3) -3|3x + 8| + 5, x = -4
-7
أحل كلاً من المعادلات الآتية، وأمثل مجموعة الحل على خط الأعداد (إن أمكن):
4) |x + 3| = 7
{-10, 4}

5) |x - 8| = 14
{-6, 22}

6) |-3x| = 15
{-5, 5}
7) |3x + 2| + 2 = 5
{-, }
8) |2x - 4| - 8 = 10
{-7, 11}
9) -4|8 – 5x| = 16
Ø
أحل كلاً من المتباينات الآتية، وأمثل مجموعة الحل على خط الأعداد (إن أمكن):
10) |x + 8| 3
[-11, -5]
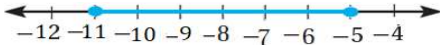
11) |2x - 5| < 9
(-2, 7)

12) |3x + 1| > 8
(-∞, -3) U ( , ∞)
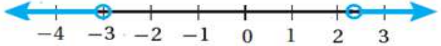
13) |3x - 1| + 6 > 0
R , (-∞, ∞)

14) 2|3x + 8| - 13 -5
[-4, -]
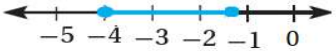
15) -3|2 – 4x| + 5 < -13
x < -1 or x > 2
(-∞, -1) U (2, ∞)
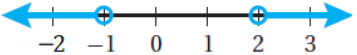
16) |6x + 2| < -4
Ø
17) 3|5x - 7| - 6 < 24
(-, )

18) |5x + 3| - 4 9
(-∞, -) U (2, ∞)

أكتب متباينة تمثل كل جملة مما يأتي، ثم أمثلها على خط الأعداد:
19) المسافة بين عدد والصفر أكبر من 7
|x| = 5
20) المسافة بين عدد و 3 أقل من أو تساوي 4
|x - 3| = 5
21) صناعة: إذا علمت أن مصنعاً ينتج علب بسكويت كتلة العلبة المثالية 454 g، وكان مراقب الجودة يستثني العلبة التي تزيد على الكتلة المثالية أو تنقص عنها بمقدار 5 g، فأكتب متباينة قيمة مطلقة أجد بها المدى المسموح به لكتل علب البسكويت.
|x| > 7

22) كرة قدم: إذا كانت الكتلة المثالية الموصى بها لكرة القدم 430 g، وكان مسموح أن تزيد على الكتلة المثالية أو تنقص عنها بمقدار 20 g، فأكتب معادلة قيمة مطلقة لإيجاد أكبر وأقل كتلة مسموح بها لكرة القدم، ثم أحلها.
|x - 3| 4

إعداد : شبكة منهاجي التعليمية
30 / 08 / 2024
النقاشات
Mousa Alabed
شكرا اااااااااااااااااااااا منهاجي
إضافة رد
0 ردود