مهارات التفكير العليا

مهارات التفكير العليا

الضرب القياسي

(37) تبرير: إذا كانت $C (- 4, 5, - 1), B (1, - 5, 9), A (3, - 2, 4)$ ، وكانت النقطة D تقع على المستقيم المار بالنقطة A والنقطة B، وكانت الزاوية CDA قائمة، فما إحداثيات النقطة D؟ أبرر إجابتي.

بما أن قائمة $∠ C D A$ ، فالنقطة D هي المسقط العمودي للنقطة C، على $\overset{\leftrightarrow}{A B}$ ، ويمكن إيجاد إحداثياتها كما يأتي:

$\vec{A B} = ⟨ - 2, - 3, 5 ⟩$

معادلة المستقيم $\overset{\leftrightarrow}{A B}$ هي: $\vec{r} = ⟨ 3, - 2, 4 ⟩ + t ⟨ - 2, - 3, 5 ⟩$

بما أن النقطة D تقع على $\overset{\leftrightarrow}{A B}$ فإن:

$\vec{O D} = ⟨ 3 - 2 t, - 2 - 3 t, 4 + 5 t ⟩ \begin{aligned} \vec{C D} = ⟨ 3 - 2 t + 4, - 2 - 3 t - 5, 4 + 5 t + 1 ⟩ = ⟨ 7 - 2 t, - 7 - 3 t, 5 + 5 t ⟩ \\ \vec{C D} ⊥ \overset{\leftrightarrow}{A B} \Rightarrow \vec{C D} \cdot \vec{A B} = 0 \\ \Rightarrow - 2 (7 - 2 t) - 3 (- 7 - 3 t) + 5 (5 + 5 t) \Rightarrow t = - \frac{16}{19} \\ \Rightarrow \vec{O D} = ⟨ 3 - 2 (- \frac{16}{19}), - 2 - 3 (- \frac{16}{19}), 4 + 5 (- \frac{16}{19}) ⟩ = ⟨ \frac{89}{19}, \frac{10}{19}, \frac{- 4}{19} ⟩ \end{aligned}$

إذن، إحداثيات D هي: $(\frac{89}{19}, \frac{10}{19}, \frac{- 4}{19})$

تحد: إذا كانت: $\vec{r} = (\begin{matrix} - 8 \\ 16 \\ 1 \end{matrix}) + t (\begin{matrix} 7 \\ - 3 \\ - 6 \end{matrix})$

معادلة متجهة للمستقيم $l_{1}$ ، وكانت $\vec{r} = (\begin{matrix} - 10 \\ 31 \\ - 26 \end{matrix}) + u (\begin{matrix} 3 \\ - 6 \\ 7 \end{matrix})$ معادلة متجهة للمستقيم $l_{2}$ ، وتقاطع هذان المستقيمان في النقطة P، وكانت النقطة Q تقع على المستقيم $l_{1}$ ، حيث: $t = 3$ ، والنقطة R تقع على المستقيم $l_{2}$ ، حيث: $P Q = P R, u > 3$ ، فأجيب عن السؤالين الآتيين تباعاً:

(38) إذا كان $m ∠ R P Q = θ$ ، فأبين أن: $\cos θ = - \frac{3}{94}$ .

الزاوية RPQ هي الزاوية المحصورة بين المستقيمين $l_{2}, l_{1}$ ، ونساوي الزاوية بين اتجاهيهما.

اتجاه $l_{1}$ هو: $\vec{u} = (\begin{matrix} 7 \\ - 3 \\ - 6 \end{matrix})$ ، واتجاه $l_{2}$ هو: $\vec{v} = (\begin{matrix} 3 \\ - 6 \\ 7 \end{matrix})$

$\begin{aligned} m ∠ R P Q = θ \Rightarrow c o s θ = \frac{\vec{u} \cdot \vec{v}}{| \vec{u} | | \vec{v} |} & = \frac{21 + 18 - 42}{\sqrt{49 + 9 + 36} \times \sqrt{9 + 36 + 49}} \\ = \frac{- 3}{\sqrt{94} \times \sqrt{94}} = \frac{- 3}{94} \end{aligned}$

(39) أبين أن مساحة المثلث PQR هي $2 \sqrt{8827}$ وحدة مربعة.

لإيجاد مساحة PQR يتعين معرفة متجهين يمثلان اثنين من أضلاعه، ولذا تلزمنا معرفة إحداثيات رؤوسيه الرأس P هو نقطة تقاطع المستقيمين $l_{2}, l_{1}$ ، ونجدها بمساواة $\vec{r}$ في المعادلتين ومساواة الإحداثيات المتناظرة:

$\begin{aligned} ⟨ - 8 + 7 t, 16 - 3 t, 1 - 6 t ⟩ = ⟨ - 10 + 3 u, 31 - 6 u, - 26 + 7 u ⟩ \\ \Rightarrow - 8 + 7 t = - 10 + 3 u \Rightarrow 7 t - 3 u = - 2 \dots \dots \dots (1) \\ 16 - 3 t = 31 - 6 u \Rightarrow - 3 t + 6 u = 15 \dots \dots \dots \dots \dots (2) \\ 1 - 6 t = - 26 + 7 u \Rightarrow 7 u + 6 t = 27 \dots \dots \dots \dots \dots \dots (3) \end{aligned}$

بحل النظام نجد أن: 3=t=1,u

لإيجاد إحداثيات P تعوض t=1 في معادلة $l_{1}$ :

$\begin{array}{r} \vec{r} = ⟨ - 8 + 7, 16 - 3, 1 - 6 ⟩ = ⟨ - 1, 13, - 5 ⟩ \\ \Rightarrow P (- 1, 13, - 5) \end{array}$

نجد إحداثيات Q بتعريض 3=t في معادلة $l_{1}$ :

$\begin{aligned} \vec{r} & = ⟨ - 8 + 21, 16 - 9, 1 - 18 ⟩ \\ \Rightarrow Q (13, 7, - 17) \end{aligned}$

النقطة R تقع على المستقيم $l_{2}$ ، فمتجه موقعها هو: $⟨ - 10 + 3 u, 31 - 6 u, - 26 + 7 u ⟩$

$\begin{aligned} \vec{P Q} = ⟨ 13, 7, - 17 ⟩ - ⟨ - 1, 13, - 5 ⟩ = ⟨ 14, - 6, - 12 ⟩ \\ \vec{P R} = ⟨ - 10 + 3 u, 31 - 6 u, - 26 + 7 u ⟩ - ⟨ - 1, 13, - 5 ⟩ \\ = ⟨ - 9 + 3 u, 18 - 6 u, - 21 + 7 u ⟩ \\ P R = P Q \Rightarrow | \vec{P R} | = | \vec{P Q} | \\ \Rightarrow (- 9 + 3 u)^{2} + (18 - 6 u)^{2} + (- 21 + 7 u)^{2} = 14^{2} + (- 6)^{2} + (- 12)^{2} \\ 94 u^{2} - 564 u + 470 = 0 \Rightarrow u^{2} - 6 u + 5 = 0 \\ \Rightarrow u = 1 أو u = 5 \end{aligned}$

لكن 3<u، فإذن 5=u وتكون $R (5, 1, 9)$

لدينا: $R (5, 1, 9), Q (13, 7, - 17), P (- 1, 13, - 5)$

$\begin{aligned} | \vec{P R} | = | \vec{P Q} | = \sqrt{14^{2} + (- 6)^{2} + (- 12)^{2}} = \\ Area (P Q R) = \frac{1}{2} | \vec{P Q} | \times | \vec{P R} | \sin θ \\ \sin θ = \sqrt{1 - \frac{9}{94^{2}}} = \sqrt{\frac{8827}{8836}} \\ Area (P Q R) = \frac{1}{2} \sqrt{376} \times \sqrt{376} \times 223 \sqrt{\frac{88}{88}} \end{aligned}$

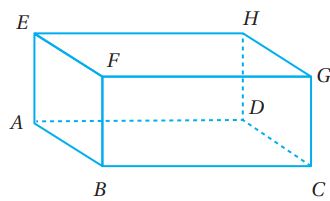
تحد: رسم متوازي المستطيلات الآتي باستعمال برمجية حاسوبية تعتمد في قياساتها على المتجهات، فكانت كالأتي:

$\vec{A B} = (2 \hat{i} + 4 \hat{j} + 4 \hat{k}), \vec{A D} = (- 10 \hat{i} + 10 \hat{j} - 5 \hat{k}), \vec{A E} = (- 6 \hat{i} - 3 \hat{j} + 6 \hat{k})$

متوازي أضلاع

(40) إذا كانت $B (8, 3, - 2)$ ، فأجد إحداثيات النقطة H.

لتكن $H (x, y, z)$

$\begin{aligned} \vec{B H} = \vec{B A} + \vec{A D} + \vec{D H} (\vec{D H} = \vec{A E}) \\ ⟨ x - 8, y - 3, z + 2 ⟩ = ⟨ - 2, - 4, - 4 ⟩ + ⟨ - 10, 10, - 5 ⟩ + ⟨ - 6, - 3, 6 ⟩ \\ \Rightarrow ⟨ x - 8, y - 3, z + 2 ⟩ = ⟨ - 18, 3, - 3 ⟩ \\ \Rightarrow x - 8 = - 18 \Rightarrow x = - 10 \\ y - 3 = 3 \Rightarrow y = 6 \\ z + 2 = - 3 \Rightarrow z = - 5 \\ \Rightarrow H (- 10, 6, - 5) \end{aligned}$

ملحوظة: توجد طرق أخرى للحل، منها التدرج بإيجاد إحداثيات A ثم E ثم H ....

(41) أجد قياس الزاوية GAC مقرباً إلى أقرب عشر درجة.

يمكن بالطرق الواردة في حل السؤال السابق إيجاد احداثيات كل من C,G وإكمال الحل لحساب قياس الزاوية المطلوبة تقليدياً، هنا سنستفيد من حقيقة أن GC وAC متعامدان (أي أن $b b b$ قائم في C)

لیکن $m ∠ G A C = θ$

$\begin{aligned} \tan θ & = \frac{| \vec{C G} |}{| \vec{A C} |} = \frac{| \vec{A E} |}{| \vec{A B} + \vec{A D} |} = \frac{| ⟨ - 6, - 3, 6 ⟩ |}{| ⟨ 2, 4, 4 ⟩ + ⟨ - 10, 10, - 5 ⟩ |} = \frac{| ⟨ - 6, - 3, 6 ⟩ |}{| ⟨ - 8, 14, - 1 ⟩ |} \\ = \frac{\sqrt{36 + 9 + 36}}{\sqrt{64 + 196 + 1}} = \frac{\sqrt{81}}{\sqrt{261}} = \frac{9}{3 \sqrt{29}} = \frac{3}{\sqrt{29}} \Rightarrow θ = \tan^{- 1} \frac{3}{\sqrt{29}} \approx {29.1}^{\circ} \end{aligned}$

(42) إذا كان X نقطة منتصف الضلع $\bar{E F}$ ، فأجد جيب تمام الزاوية DXC.

$\begin{aligned} \vec{X D} & = \vec{X E} + \vec{E A} + \vec{A D} \\ = \frac{1}{2} \vec{F E} - \vec{A E} + \vec{A D} \\ = - \frac{1}{2} \vec{A B} - \vec{A E} + \vec{A D} \\ = ⟨ - 1, - 2, - 2 ⟩ - ⟨ - 6, - 3, 6 ⟩ + ⟨ - 10, 10, - 5 ⟩ \\ = ⟨ - 5, 11, - 13 ⟩ \end{aligned} \begin{aligned} ⟹ | \vec{X D} | = \sqrt{25 + 121 + 169} = \sqrt{315} \\ \vec{X C} = \vec{X F} + \vec{F B} + \vec{B C} \\ = \frac{1}{2} \vec{E F} - \vec{A E} + \vec{A D} \\ = \frac{1}{2} \vec{A B} - \vec{A E} + \vec{A D} \\ = ⟨ 1, 2, 2 ⟩ - ⟨ - 6, - 3, 6 ⟩ + ⟨ - 10, 10, - 5 ⟩ \\ = ⟨ - 3, 15, - 9 ⟩ \end{aligned} \begin{aligned} \Rightarrow | \vec{X D} | = \sqrt{9 + 225 + 81} = \sqrt{315} \\ \vec{X D} \cdot \vec{X C} = - 5 (- 3) + 11 (15) - 13 (- 9) = 297 \\ c o s θ = \frac{\vec{X D} \cdot \vec{X C}}{| \vec{X D} | | \vec{X C} |} = \frac{297}{315} = \frac{33}{35} \end{aligned}$

إعداد : شبكة منهاجي التعليمية

10 / 07 / 2023

النقاشات

جميع الحقوق محفوظة © 2024