أتدرب وأحل المسائل
التكامل بالأجزاء
أجد كلاً من التكاملات الآتية:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
ملاحظة: لإيجاد v استخدمنا طريقة التعويض، حيث: ومنه:
(10)
هذه المسألة يمكن حلها بالتعويض، حيث:
وحلها بالأجزاء كالآتي:
(11)
بالأجزاء 3 مرات، لنستخدم طريقة الجدول:
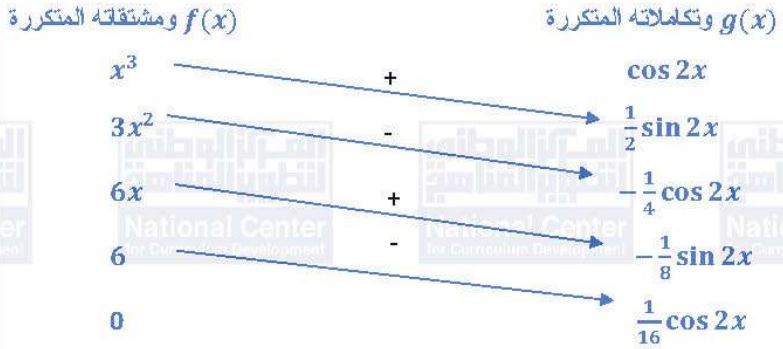
(12)
(13)
(14)
(15)
أجد قيمة كل من التكاملات الآتية:
(16)
(17)
(18)
نجد بطريقة الأجزاء:
(19)
(20)
(21)
نجد باستخدام طريقة الجدول:
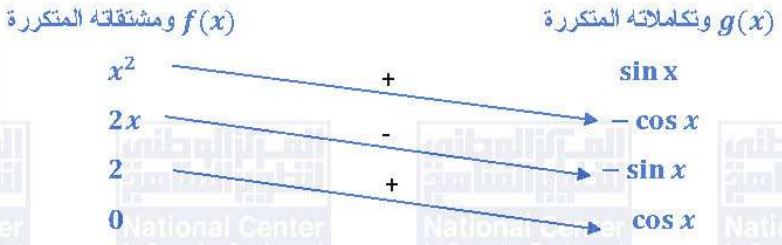
(22)
(23)
(24)
أجد كلاً من التكاملات الآتية:
(25)
(27)
(28)
(29)
(30)
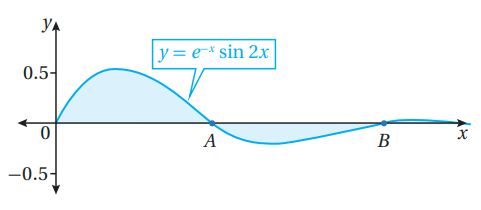 إذا كان الشكل المجاور يمثل منحنى الاقتران: ، حيث: فأجيب عن الأسئلة الثلاثة الآتية تباعاً:
إذا كان الشكل المجاور يمثل منحنى الاقتران: ، حيث: فأجيب عن الأسئلة الثلاثة الآتية تباعاً:
(31) أجد إحداثيي كل من النقطة ، والنقطة .
الإحداثيان x للنقطتين A وB هما أصغر حلين موجبين للمعادلة:
(32) أجد مساحة المنطقة المظللة.
للبسيط سنجد أولاً: (التكامل غير المحدود)
(33) يتحرك جسيم في مسار مستقيم، وتعطى سرعته المتجهة بالاقتران: ، حيث الزمن بالثواني، و سرعته المتجهة بالمتر لكل ثانية. إذا بدأ الجسيم الحركة من نقطة الأصل، فأجد موقعه بعد ثانية.
في كل مما يأتي المشتقة الأولى للاقتران ، ونقطة يمر بها منحنى . أستعمل المعلومات المعطاة لإيجاد قاعدة الاقتران :
(34)
(35)
 (36) دورة تدريبية: تقدمت دعاء لدورة تدريبية متقدمة في الطباعة. إذا كان عدد الكلمات التي تطبعها دعاء في الدقيقة يزداد بمعدل: ، حيث عدد الكلمات التي تطبعها دعاء في الدقيقة بعد أسبوعاً من التحاقها بالدورة، فأجد ، علماً بأن دعاء كانت تطبع 40 كلمة في الدقيقة عند بدء الدورة.
(36) دورة تدريبية: تقدمت دعاء لدورة تدريبية متقدمة في الطباعة. إذا كان عدد الكلمات التي تطبعها دعاء في الدقيقة يزداد بمعدل: ، حيث عدد الكلمات التي تطبعها دعاء في الدقيقة بعد أسبوعاً من التحاقها بالدورة، فأجد ، علماً بأن دعاء كانت تطبع 40 كلمة في الدقيقة عند بدء الدورة.




النقاشات