أتدرب وأحل المسائل

أتدرب وأحل المسائل

التكامل

أجد كلاً من التكاملات الآتية:

$\int x^{2} {(2 x^{3} + 5)}^{4} d x$ (1)

$\begin{aligned} u = 2 x^{3} + 5 \Rightarrow & \frac{d u}{d x} = 6 x^{2} \Rightarrow d x = \frac{d u}{6 x^{2}} \\ \int x^{2} {(2 x^{3} + 5)}^{4} d x & = \int x^{2} u^{4} \times \frac{d u}{6 x^{2}} \\ = \int \frac{1}{6} u^{4} d u \\ = \frac{1}{30} u^{5} + C \\ = \frac{1}{30} {(2 x^{3} + 5)}^{5} + C \end{aligned}$

$\int x^{2} \sqrt{x + 3} d x$ (2)

$\begin{aligned} u = x + 3 \Rightarrow d x = d u, x = u - 3 \\ \begin{aligned} x^{2} \sqrt{x + 3} d x & = \int x^{2} \sqrt{u} d u \\ = \int (u - 3)^{2} \sqrt{u} d u \\ = \int (u^{\frac{5}{2}} - 6 u^{\frac{3}{2}} + 9 u^{\frac{1}{2}}) d u \\ = \frac{2}{7} u^{\frac{7}{2}} - \frac{12}{5} u^{\frac{5}{2}} + 6 u^{\frac{3}{2}} + C \\ = \frac{2}{7} (x + 3)^{\frac{7}{2}} - \frac{12}{5} (x + 3)^{\frac{5}{2}} + 6 (x + 3)^{\frac{3}{2}} + C \\ = \frac{2}{7} \sqrt{(x + 3)^{7}} - \frac{12}{5} \sqrt{(x + 3)^{5}} + 6 \sqrt{(x + 3)^{3}} + C \end{aligned} \end{aligned}$

$\int x (x + 2)^{3} d x$ (3)

$\begin{aligned} u = x + 2 \Rightarrow d x = d u, x = u - 2 \\ \int x (x + 2)^{3} d x = \int x u^{3} d u \\ = \int (u - 2) u^{3} d u \\ = \int (u^{4} - 2 u^{3}) d u \\ = \frac{1}{5} u^{5} - \frac{1}{2} u^{4} + C \\ = \frac{1}{5} (x + 2)^{5} - \frac{1}{2} (x + 2)^{4} + C \end{aligned}$

$\int \frac{x}{\sqrt{x + 4}} d x$ (4)

$\begin{aligned} u = x + 4 & \Rightarrow d x = d u, x = u - 4 \\ \int \frac{x}{\sqrt{x + 4}} d x & = \int \frac{x}{\sqrt{u}} d u \\ = \int \frac{u - 4}{\sqrt{u}} d u \\ = \int (u^{\frac{1}{2}} - 4 u^{- \frac{1}{2}}) d u \\ = \frac{2}{3} u^{\frac{3}{2}} - 8 u^{\frac{1}{2}} + C \\ = \frac{2}{3} (x + 4)^{\frac{3}{2}} - 8 (x + 4)^{\frac{1}{2}} + C \\ = \frac{2}{3} \sqrt{(x + 4)^{3}} - 8 \sqrt{x + 4} + C \end{aligned}$

$\int \sin x \cos 2 x d x$ (5)

$\begin{aligned} \int \sin x \cos 2 x d x = \int \sin x (2 \cos^{2} x - 1) d x \\ u = \cos x \Rightarrow \frac{d u}{d x} = - \sin x \Rightarrow d x = \frac{d u}{- \sin x} \\ \int \sin x \cos 2 x d x = \int \sin x (2 u^{2} - 1) \times \frac{d u}{- \sin x} \\ = \int (1 - 2 u^{2}) d u \\ = u - \frac{2}{3} u^{3} + C \\ = \cos x - \frac{2}{3} \cos^{3} x + C \end{aligned}$

$\int \frac{e^{3 x}}{e^{x} + 1} d x$ (6)

$b b b \begin{aligned} u = e^{x} + 1 & \Rightarrow \frac{d u}{d x} = e^{x} \Rightarrow d x = \frac{d u}{e^{x}}, e^{x} = u - 1 \\ \int \frac{e^{3 x}}{e^{x} + 1} d x & = \int \frac{e^{3 x}}{u} \times \frac{d u}{e^{x}} \\ = \int \frac{e^{2 x}}{u} d u \\ = \int \frac{(u - 1)^{2}}{u} d u \\ = \int (u - 2 + \frac{1}{u}) d u \\ = \frac{1}{2} u^{2} - 2 u + \ln | u | + C \\ = \frac{1}{2} {(e^{x} + 1)}^{2} - 2 (e^{x} + 1) + \ln (e^{x} + 1) + C \end{aligned}$

$\int \sec^{4} x d x$ (7)

$\begin{aligned} \int \sec^{4} x d x & = \int \sec^{2} x \times \sec^{2} x d x = \int \sec^{2} x (1 + \tan^{2} x) d x \\ u = \tan x & \Rightarrow \frac{d u}{d x} = \sec^{2} x \Rightarrow d x = \frac{d u}{\sec^{2} x} \\ \int \sec^{4} x d x & = \int \sec^{2} x (1 + u^{2}) \times \frac{d u}{\sec^{2} x} \\ = \int (1 + u^{2}) d u \\ = u + \frac{1}{3} u^{3} + C \\ = \tan x + \frac{1}{3} \tan^{3} x + C \end{aligned}$

$\int \frac{\tan x}{\cos^{2} x} d x$ (8)

$\begin{aligned} \int \frac{\tan x}{\cos^{2} x} d x & = \int \tan x \sec^{2} x d x \\ u = \tan x & \Rightarrow \frac{d u}{d x} = \sec^{2} x \Rightarrow d x = \frac{d u}{\sec^{2} x} \\ \int \frac{\tan x}{\cos^{2} x} d x & = \int u \sec^{2} x \times \frac{d u}{\sec^{2} x} \\ = \int u d u \\ = \frac{1}{2} u^{2} + C \\ = \frac{1}{2} \tan^{2} x + C \end{aligned}$

$\int \frac{\sin (\ln x)}{x} d x$ (9)

$\begin{aligned} u = \ln x \Rightarrow \frac{d u}{d x} = \frac{1}{x} \Rightarrow d x = x d u \\ \int \frac{\sin (\ln x)}{x} d x = \int \frac{\sin u}{x} \times x d u \\ = \int \sin u d u \\ = - \cos u + C \\ = - \cos (\ln x) + C \end{aligned}$

$\int \frac{\sin x \cos x}{1 + \sin^{2} x} d x$ (10)

$\begin{aligned} \int \frac{\sin x \cos x}{1 + \sin^{2} x} d x & = \frac{1}{2} \int \frac{2 \sin x \cos x}{1 + \sin^{2} x} d x \\ = \frac{1}{2} \ln (1 + \sin^{2} x) + C \end{aligned}$

$\int \frac{2 e^{x} - 2 e^{- x}}{{(e^{x} + e^{- x})}^{2}} d x$ (11)

$\begin{aligned} u = e^{x} + e^{- x} \Rightarrow \frac{d u}{d x} = e^{x} - e^{- x} \Rightarrow d x = \frac{d u}{e^{x} - e^{- x}} \\ \int \frac{2 e^{x} - 2 e^{- x}}{{(e^{x} + e^{- x})}^{2}} d x = \int \frac{2 (e^{x} - e^{- x})}{u^{2}} \times \frac{d u}{e^{x} - e^{- x}} \\ = \int 2 u^{- 2} d u \\ = - 2 u^{- 1} + C \\ = - \frac{2}{e^{x} + e^{- x}} + C \end{aligned}$

$\int \frac{- x}{(x + 1) \sqrt{x + 1}} d x$ (12)

$\begin{aligned} u = x + 1 ⟹ d x & = d u, x = u - 1 \\ \int \frac{- x}{(x + 1) \sqrt{x + 1}} d x & = \int \frac{1 - u}{u \sqrt{u}} d u \\ = \int \frac{1 - u}{u^{\frac{3}{2}}} d u \\ = \int (u^{- \frac{3}{2}} - u^{- \frac{1}{2}}) d u \\ = - 2 u^{- \frac{1}{2}} - 2 u^{\frac{1}{2}} + C \\ = - 2 (x + 1)^{- \frac{1}{2}} - 2 (x + 1)^{\frac{1}{2}} + C \\ = \frac{- 2}{\sqrt{x + 1}} - 2 \sqrt{x + 1} + C \end{aligned}$

$\int x \sqrt[3]{x + 10} d x$ (13)

$\begin{aligned} u = x + 10 \Rightarrow & d x = d u, x = u - 10 \\ \int x \sqrt[3]{x + 10} d x & = \int (u - 10) u^{\frac{1}{3}} d u \\ = \int (u^{\frac{4}{3}} - 10 u^{\frac{1}{3}}) d u \\ = \frac{3}{7} u^{\frac{7}{3}} - \frac{15}{2} u^{\frac{4}{3}} + C \\ = \frac{3}{7} (x + 10)^{\frac{7}{3}} - \frac{15}{2} (x + 10)^{\frac{4}{3}} + C \\ = \frac{3}{7} \sqrt[3]{(x + 10)^{7}} - \frac{15}{2} \sqrt[3]{(x + 10)^{4}} + C \end{aligned}$

$\int (\sec^{2} \frac{x}{2} \tan^{7} \frac{x}{2}) d x$ (14)

$\begin{aligned} u = \tan \frac{x}{2} \Rightarrow \frac{d u}{d x} & = \frac{1}{2} \sec^{2} \frac{x}{2} \Rightarrow d x = \frac{2 d u}{\sec^{2} \frac{x}{2}} \\ \int \sec^{2} \frac{x}{2} \tan^{7} \frac{x}{2} d x & = \int \sec^{2} \frac{x}{2} u^{7} \times \frac{2 d u}{\sec^{2} \frac{x}{2}} \\ = 2 \int u^{7} d u \\ = \frac{1}{4} u^{8} + C \\ = \frac{1}{4} \tan^{8} \frac{x}{2} + C \end{aligned}$

$\int \frac{\sec^{3} x + e^{\sin x}}{\sec x} d x$ (15)

$\begin{aligned} \int \frac{\sec^{3} x + e^{\sin x}}{\sec x} d x = \int (\sec^{2} x + \cos x e^{\sin x}) d x \\ = \int \sec^{2} x d x + \int \cos x e^{\sin x} d x \\ u = \sin x \Rightarrow \frac{d u}{d x} = \cos x \Rightarrow d x = \frac{d u}{\cos x} \\ \int \frac{\sec^{3} x + e^{\sin x}}{\sec x} d x = \int \sec^{2} x d x + \int \cos x e^{u} \times \frac{d u}{\cos x} \\ = \tan x + \int e^{u} d u \\ = \tan x + e^{u} + C \\ = \tan x + e^{\sin x} + C \end{aligned}$

$\int (1 + \sqrt[3]{\sin x}) \cos^{3} x d x$ (16)

$\begin{aligned} u = \sin x \Rightarrow \frac{d u}{d x} = \cos x & \Rightarrow d x = \frac{d u}{\cos x} \\ \int (1 + \sqrt[3]{\sin x}) \cos^{3} x d x & = \int (1 + u^{\frac{1}{3}}) \cos^{3} x \frac{d u}{\cos x} \\ = \int (1 + u^{\frac{1}{3}}) \cos^{2} x d u \\ = \int (1 + u^{\frac{1}{3}}) (1 - \sin^{2} x) d u \\ = \int (1 + u^{\frac{1}{3}}) (1 - u^{2}) d u \\ = \int (1 + u^{\frac{1}{3}}) (1 - u^{2}) d u \\ = \int (1 - u^{2} + u^{\frac{1}{3}} - u^{\frac{7}{3}}) d u \\ = u - \frac{1}{3} u^{3} + \frac{3}{4} u^{\frac{4}{3}} - \frac{3}{10} u^{\frac{10}{3}} + C \\ = \sin x - \frac{1}{3} \sin^{3} x + \frac{3}{4} & \sin^{\frac{4}{3}} x - \frac{3}{10} \sin^{\frac{10}{3}} x + C \end{aligned}$

$\int \sin x \sec^{5} x d x$ (17)

$\begin{aligned} \int \sin x \sec^{5} x d x = \int \sin x \cos^{- 5} x d x \\ u = \cos x \Rightarrow \frac{d u}{d x} = - \sin x \Rightarrow d x = \frac{d u}{- \sin x} \\ \int \sin x \sec^{5} x d x = \int \sin x u^{- 5} \times \frac{d u}{- \sin x} \\ = - \int u^{- 5} d u \\ = \frac{1}{4} u^{- 4} + C \\ = \frac{1}{4} \cos^{- 4} x + C \\ = \frac{1}{4} \sec^{4} x + C \end{aligned}$

$\int \frac{\sin x + \tan x}{\cos^{3} x} d x$ (18)

$\begin{aligned} \int \frac{\sin x + \tan x}{\cos^{3} x} d x & = \int (\tan x \sec^{2} x + \tan x \sec^{3} x) d x \\ = \int \tan x \sec x (\sec x + \sec^{2} x) d x \\ u = \sec x \Rightarrow \frac{d u}{d x} & = \tan x \sec x \Rightarrow d x = \frac{d u}{\tan x \sec x} \\ \int \frac{\sin x + \tan x}{\cos^{3} x} d x & = \int \tan x \sec x (u + u^{2}) \frac{d u}{\tan x \sec x} \\ = \int (u + u^{2}) d u \\ = \frac{1}{2} u^{2} + \frac{1}{3} u^{3} + C \\ = \frac{1}{2} \sec^{2} x + \frac{1}{3} \sec^{3} x + C \end{aligned}$

أجد قيمة كلا من التكاملات الآتية:

$\int_{0}^{π / 4} \sin x \sqrt{1 - \cos^{2} 2 x} d x$ (19)

$\sqrt{1 - \cos^{2} 2 x} = \sqrt{\sin^{2} 2 x} = | \sin 2 x |$

لكن الزاوية $2 x$ تكون ضمن الربع الأول عندما $0 < x < \frac{π}{4}$

لذا فإن $\sin 2 x > 0$ ويكون $| \sin 2 x | = \sin 2 x$

$\begin{aligned} \int_{0}^{\frac{π}{4}} \sin x \sqrt{1 - \cos^{2} 2 x} d x = \int_{0}^{\frac{π}{4}} \sin x \sin 2 x d x \\ = \int_{0}^{\frac{π}{4}} 2 \sin^{2} x \cos x d x \\ u = \sin x \Rightarrow \frac{d u}{d x} = \cos x \Rightarrow d x = \frac{d u}{\cos x} \\ x = 0 \Rightarrow u = 0 \\ x = \frac{π}{4} \Rightarrow u = \frac{1}{\sqrt{2}} \\ \int_{0}^{\frac{π}{4}} \sin x \sqrt{1 - \cos^{2} 2 x} d x = \int_{0}^{\frac{1}{\sqrt{2}}} 2 u^{2} \cos x \frac{d u}{\cos x} \\ = \int_{0}^{\frac{1}{\sqrt{2}}} 2 u^{2} d u \\ = {\frac{2}{3} u^{3} |}_{0}^{\frac{1}{\sqrt{2}}} \\ = \frac{1}{3 \sqrt{2}} \end{aligned}$

$\int_{0}^{π / 2} x \sin x^{2} d x$ (20)

$\begin{aligned} u = x^{2} \Rightarrow \frac{d u}{d x} = 2 x \Rightarrow d x = \frac{d u}{2 x} \\ x = \frac{π}{2} \Rightarrow u = \frac{π^{2}}{4} \\ x = 0 \Rightarrow u = 0 \\ \int_{0}^{\frac{π}{2}} x \sin x^{2} d x = \int_{0}^{\frac{π^{2}}{4}} x \sin u \frac{d u}{2 x} \\ = \frac{1}{2} \int_{0}^{\frac{π^{2}}{4}} \sin u d u \\ = - {\frac{1}{2} \cos u |}_{0}^{\frac{π^{2}}{4}} \\ = - \frac{1}{2} (\cos \frac{π^{2}}{4} - 1) \approx 0.891 \end{aligned}$

$\int_{0}^{1} \frac{x^{3}}{\sqrt{1 + x^{2}}} d x$ (21)

$\begin{aligned} u = 1 + x^{2} \Rightarrow \frac{d u}{d x} = 2 x \Rightarrow d x = \frac{d u}{2 x}, x^{2} = u - 1 \\ x = 0 \Rightarrow u = 1 \\ x = 1 \Rightarrow u = 2 \\ \int_{0}^{1} \frac{x^{3}}{\sqrt{1 + x^{2}}} d x = \int_{1}^{2} \frac{x^{3}}{\sqrt{u}} \times \frac{d u}{2 x} = \frac{1}{2} \int_{1}^{2} \frac{x^{2}}{\sqrt{u}} d u = \frac{1}{2} \int_{1}^{2} \frac{u - 1}{\sqrt{u}} d u \\ = \frac{1}{2} \int_{1}^{2} (u^{\frac{1}{2}} - u^{- \frac{1}{2}}) d u \\ = {\frac{1}{2} (\frac{2}{3} u^{\frac{3}{2}} - 2 u^{\frac{1}{2}}) |}_{1}^{2} \\ = \frac{1}{2} (\frac{2}{3} (2)^{\frac{3}{2}} - 2 (2)^{\frac{1}{2}} - (\frac{2}{3} (1) - 2 (1))) \\ = \frac{2 - \sqrt{2}}{3} \end{aligned}$

$\int_{0}^{π / 3} \sec^{2} x \tan^{5} x d x$ (22)

$\begin{aligned} u = t a n x \Rightarrow \frac{d u}{d x} = s e c^{2} x \Rightarrow d x = \frac{d u}{s e c^{2} x} \\ x = 0 \Rightarrow u = 0 \\ x = \frac{π}{3} \Rightarrow u = \sqrt{3} \\ \int_{0}^{\frac{π}{3}} s e c^{2} x t a n^{5} x d x = \int_{0}^{\sqrt{3}} s e c^{2} x u^{5} \frac{d u}{s e c^{2} x} \\ = \int_{0}^{\sqrt{3}} u^{5} d u \\ = {\frac{1}{6} u^{6} |}_{0}^{\sqrt{3}} \\ = \frac{9}{2} \end{aligned}$

$\int_{0}^{2} (x - 1) e^{(x - 1)^{2}} d x$ (23)

$\begin{aligned} u = (x - 1)^{2} \Rightarrow \frac{d u}{d x} = 2 (x - 1) \Rightarrow d x = \frac{d u}{2 (x - 1)} \\ x = 0 \Rightarrow u = 1 \\ x = 2 \Rightarrow u = 1 \\ \int_{0}^{2} (x - 1) e^{(x - 1)^{2}} d x = \int_{1}^{1} (x - 1) e^{u} \frac{d u}{2 (x - 1)} = 0 \end{aligned}$

$\int_{1}^{4} \frac{\sqrt{2 + \sqrt{x}}}{\sqrt{x}} d x$ (24)

$\begin{aligned} u = 2 + \sqrt{x} \Rightarrow \frac{d u}{d x} = \frac{1}{2 \sqrt{x}} \Rightarrow d x = 2 \sqrt{x} d u \\ x = 1 \Rightarrow u = 3 \\ x = 4 \Rightarrow u = 4 \\ \int_{1}^{4} \frac{\sqrt{2 + \sqrt{x}}}{\sqrt{x}} d x = \int_{3}^{4} \frac{\sqrt{u}}{\sqrt{x}} 2 \sqrt{x} d u = \int_{3}^{4} 2 \sqrt{u} d u = {\frac{4}{3} u^{\frac{3}{2}} |}_{3}^{4} = \frac{4 (8 - 3 \sqrt{3})}{3} \end{aligned}$

$\int_{0}^{1} \frac{10 \sqrt{x}}{{(1 + \sqrt{x^{3}})}^{2}} d x$ (25)

$\begin{aligned} u = 1 + x^{\frac{3}{2}} \Rightarrow \frac{d u}{d x} = \frac{3}{2} x^{\frac{1}{2}} \Rightarrow d x = \frac{2}{3} \frac{d u}{x^{\frac{1}{2}}} \\ x = 0 \Rightarrow u = 1 \\ x = 1 \Rightarrow u = 2 \\ \int_{0}^{1} \frac{10 \sqrt{x}}{{(1 + \sqrt{x^{3}})}^{2}} d x = \int_{1}^{2} \frac{10 \sqrt{x}}{u^{2}} \frac{2}{3} \frac{d u}{x^{\frac{1}{2}}} \\ = \frac{20}{3} \int_{1}^{2} u^{- 2} d u = - {\frac{20}{3} u^{- 1} |}_{1}^{2} = \frac{10}{3} \end{aligned}$

$\int_{0}^{π / 6} 2^{\cos x} \sin x d x$ (26)

$\begin{aligned} u = \cos x \Rightarrow \frac{d u}{d x} = - \sin x \Rightarrow d x = \frac{d u}{- \sin x} \\ x = 0 \Rightarrow u = 1 \\ x = \frac{π}{6} \Rightarrow u = \frac{\sqrt{3}}{2} \\ \int_{0}^{\frac{π}{6}} 2^{\cos x} \sin x d x = \int_{1}^{\frac{\sqrt{3}}{2}} 2^{u} \sin x \frac{d u}{- \sin x} \\ = - \int_{1}^{\frac{\sqrt{3}}{2}} 2^{u} d u \\ = - {\frac{2^{u}}{\ln 2} |}_{1}^{\frac{\sqrt{3}}{2}} \\ = - \frac{1}{\ln 2} (2^{\frac{\sqrt{3}}{2}} - 2) \approx 0.256 \end{aligned}$

$\int_{π / 4}^{π / 2} \csc^{2} x \cot^{5} x d x$ (27)

$\begin{aligned} u = \cot x \Rightarrow \frac{d u}{d x} = - \csc^{2} x \Rightarrow d x = \frac{d u}{- \csc^{2} x} \\ x = \frac{π}{2} \Rightarrow u = 0 \\ x = \frac{π}{4} \Rightarrow u = 1 \\ \int_{\frac{π}{4}}^{\frac{π}{2}} \csc^{2} x \cot^{5} x d x = \int_{1}^{0} \csc^{2} x u^{5} \frac{d u}{- \csc^{2} x} \\ = \int_{1}^{0} - u^{5} d u \\ = - {\frac{1}{6} u^{6} |}_{1}^{0} \\ = \frac{1}{6} \end{aligned}$

أجد مساحة المنطقة المظللة في كل من التمثيلات البيانية الآتية:

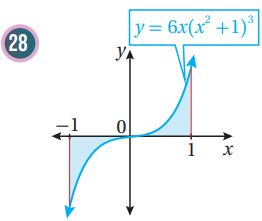
التمثيل البياني للسؤال 28

$\begin{aligned} A = - \int_{- 1}^{0} 6 x {(x^{2} + 1)}^{3} d x + \int_{0}^{1} 6 x {(x^{2} + 1)}^{3} d x \\ u = x^{2} + 1 \Rightarrow \frac{d u}{d x} = 2 x \Rightarrow d x = \frac{d u}{2 x} \\ x = - 1 \Rightarrow u = 2 \\ x = 0 \Rightarrow u = 1 \\ x = 1 \Rightarrow u = 2 \\ A = - \int_{2}^{1} 6 x u^{3} \frac{d u}{2 x} + \int_{1}^{2} 6 x u^{3} \frac{d u}{2 x} \\ = \int_{1}^{2} 3 u^{3} d u + \int_{1}^{2} 3 u^{3} d u = \int_{1}^{2} 6 u^{3} d u \\ = {\frac{6}{4} u^{4} |}_{1}^{2} \\ = \frac{45}{2} \end{aligned}$

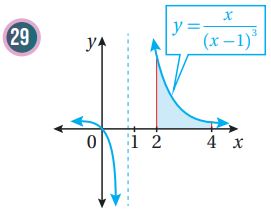
التمثيل البياني للسؤال 29

$\begin{aligned} A = \int_{2}^{4} \frac{x}{(x - 1)^{3}} d x \\ u = x - 1 \Rightarrow d x = d u, x = u + 1 \\ x = 2 \Rightarrow u = 1 \\ x = 4 \Rightarrow u = 3 \\ \begin{aligned} A = \int_{2}^{4} \frac{x}{(x - 1)^{3}} d x & = \int_{1}^{3} \frac{u + 1}{u^{3}} d u \\ = \int_{1}^{3} (u^{- 2} + u^{- 3}) d u = {(- u^{- 1} - \frac{1}{2} u^{- 2}) |}_{1}^{3} \\ = - \frac{1}{3} - \frac{1}{2} (\frac{1}{9}) + 1 + \frac{1}{2} \\ = \frac{10}{9} \end{aligned} \end{aligned}$

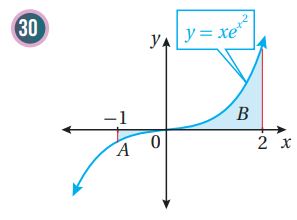
التمثيل البياني للسؤال 30

$\begin{aligned} u = x^{2} ⟹ \frac{d u}{d x} = 2 x ⟹ d x = \frac{d u}{2 x} \\ x = - 1 \Rightarrow u = 1 \\ x = 0 \Rightarrow u = 0 \\ x = 2 \Rightarrow u = 4 \\ A = - \int_{- 1}^{0} x e^{x^{2}} d x + \int_{0}^{2} x e^{x^{2}} d x = - \int_{1}^{0} x e^{u} \frac{d u}{2 x} + \int_{0}^{4} x e^{u} \frac{d u}{2 x} \\ = - \int_{1}^{0} \frac{1}{2} e^{u} d u + \int_{0}^{4} \frac{1}{2} e^{u} d u \\ = - {\frac{1}{2} e^{u} |}_{1}^{0} + {\frac{1}{2} e^{u} |}_{0}^{4} \\ = - \frac{1}{2} e^{0} + \frac{1}{2} e^{1} + \frac{1}{2} e^{4} - \frac{1}{2} e^{0} \\ = \frac{1}{2} (e^{4} + e) - 1 \approx 27.658 \end{aligned}$

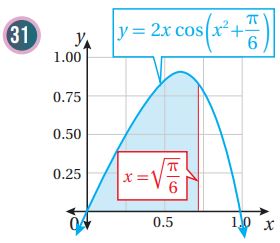
التمثيل البياني للسؤال 31

$\begin{aligned} u = x^{2} + \frac{π}{6} \Rightarrow \frac{d u}{d x} = 2 x \Rightarrow d x = \frac{d u}{2 x} \\ x = \sqrt{\frac{π}{6}} \Rightarrow= \frac{π}{3} \\ x = 0 \Rightarrow u = \frac{π}{6} \\ \begin{aligned} A = \int_{0}^{\sqrt{\frac{π}{6}}} 2 x & \cos (x^{2} + \frac{π}{6}) d x = \int_{\frac{π}{6}}^{\frac{π}{3}} 2 x \cos u \frac{d u}{2 x} \\ = \int_{\frac{π}{6}}^{\frac{π}{3}} \cos u d u \\ = {\sin u |}_{\frac{π}{6}}^{\frac{π}{3}} \\ = \sin \frac{π}{3} - \sin \frac{π}{6} \\ = \frac{\sqrt{3}}{2} - \frac{1}{2} = \frac{\sqrt{3} - 1}{2} \approx 0.366 \end{aligned} \end{aligned}$

في كل مما يأتي المشتقة الأولى للاقتران $f (x)$ ، ونقطة يمر بها منحنى $y = f (x)$ . أستعمل المعلومات المعطاة لإيجاد قاعدة الاقتران $f (x)$ :

$f^{'} (x) = 2 x {(4 x^{2} - 10)}^{2}; (2, 10)$ (32)

$\begin{aligned} f (x) = \int f^{'} (x) d x = \int 2 x {(4 x^{2} - 10)}^{2} d x \\ u = 4 x^{2} - 10 \Rightarrow \frac{d u}{d x} = 8 x \Rightarrow d x = \frac{d u}{8 x} \\ f (x) = \int 2 x u^{2} \frac{d u}{8 x} = \int u^{2} \frac{d u}{4} \\ = \frac{1}{4} \int u^{2} d u \\ = \frac{1}{12} u^{3} + C \\ \Rightarrow f (x) = \frac{1}{12} {(4 x^{2} - 10)}^{3} + C \\ f (2) = \frac{1}{12} (216) + C = 10 \Rightarrow C = - 8 \\ 10 = 18 + C \Rightarrow C = - 8 \\ \Rightarrow f (x) = \frac{1}{12} {(4 x^{2} - 10)}^{3} - 8 \end{aligned}$

$f^{'} (x) = x^{2} e^{- 0.2 x^{3}}; (0, \frac{3}{2})$ (33)

$\begin{aligned} f (x) = \int f^{'} (x) d x = \int x^{2} e^{- 0.2 x^{3}} d x \\ u = - 0.2 x^{3} \Rightarrow \frac{d u}{d x} = - 0.6 x^{2} \Rightarrow d x = \frac{d u}{- 0.6 x^{2}} \\ f (x) = \int x^{2} e^{u} \frac{d u}{- 0.6 x^{2}} = - \frac{10}{6} \int e^{u} d u \\ = - \frac{5}{3} e^{u} + C \\ \Rightarrow f (x) = - \frac{5}{3} e^{- 0.2 x^{3}} + C \\ f (0) = - \frac{5}{3} + C \\ \frac{3}{2} = - \frac{5}{3} + C \Rightarrow C = \frac{19}{6} \\ \Rightarrow f (x) = - \frac{5}{3} e^{- 0.2 x^{3}} + \frac{19}{6} \end{aligned}$

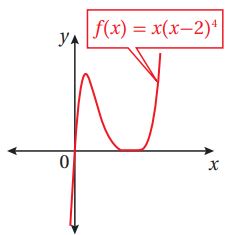يبين الشكل المجاور جزءاً من منحنى الاقتران $f (x) = x (x - 2)^{4}$ :

(34) أجد إحداثي نقطة تماس الاقتران مع المحور $x$

نجد أصفار الاقتران بحل المعادلة $f (x) = 0$

$x (x - 2)^{4} = 0 \Rightarrow x = 0, x = 2$

نقطة التقاطع $(0, 0)$ ، فتكون نقطة التماس $(2, 0)$

ويمكن التحقق بحساب $f^{'} (2)$ :

$\begin{aligned} f^{'} (x) = (x - 2)^{4} + 4 x (x - 2)^{3} \\ f^{'} (2) = (2 - 2)^{4} + 4 (2) (2 - 2)^{3} = 0 \end{aligned}$

(35) أجد مساحة المنطقة المحصورة بين منحنى الاقتران $f (x)$ والمحور $x$

$\begin{aligned} A = \int_{0}^{2} x (x - 2)^{4} d x \\ u = x - 2 \Rightarrow d x = d u, x = u + 2 \\ x = 0 \Rightarrow u = - 2 \\ x = 2 \Rightarrow u = 0 \\ \begin{aligned} A = \int_{0}^{2} x (x - 2)^{4} d x & = \int_{- 2}^{0} (u + 2) u^{4} d u \\ = \int_{- 2}^{0} (u^{5} + 2 u^{4}) d u = {(\frac{1}{6} u^{6} + \frac{2}{5} u^{5}) |}_{- 2}^{0} \\ = 0 - (\frac{1}{6} (- 2)^{6} + \frac{2}{5} (- 2)^{5}) = \frac{32}{15} \end{aligned} \end{aligned}$

(36) يتحرك جسيم في مسار مستقيم، وتعطى سرعته المتجهة بالاقتران: $v (t) = \sin ω t \cos^{2} ω t$ ، حيث $t$ الزمن بالثواني، و $v$ سرعته المتجهة بالمتر لكل ثانية، و $b b b$ ثابت، إذا انطلق الجسيم من نقطة الأصل، فأجد موقعه بعد $t$ ثانية.

$\begin{aligned} s (t) = \int \sin ω t \cos^{2} ω t d t \\ u = \cos ω t \Rightarrow \frac{d u}{d x} = - ω \sin ω t \Rightarrow d t = \frac{d u}{- ω \sin ω t} \\ s (t) = \int \sin ω t u^{2} \frac{d u}{- ω \sin ω t} \\ = \frac{- 1}{ω} \int u^{2} d u = \frac{- 1}{3 ω} u^{3} + C \\ \Rightarrow s (t) = - \frac{1}{30} \cos^{3} ω t + C \end{aligned}$

لكن $s (0) = 0$ لأن الجسيم انطلق من نقطة الأصل.

$\begin{aligned} s (0) = - \frac{1}{3 ω} + C \\ 0 = - \frac{1}{3 ω} + C \Rightarrow C = \frac{1}{3 ω} \\ \Rightarrow s (t) = - \frac{1}{3 ω} \cos^{3} ω t + \frac{1}{3 ω} \end{aligned}$

(37) طب: يمثل الاقتران $C (t)$ تركيز دواء في الدم بعد $t$ دقيقة من حقنه في جسم مريض، حيث $C$ مقيسة بالمليغرام لكل سنتيمتر مكعب $(mg / {cm}^{3})$ ، إذا كان تركيز الدواء لحظة حقنه في جسم المريض $0.5 mg / {cm}^{3}$ ، وأخذ يتغير بمعدل $C^{'} (t) = \frac{- 0.01 e^{- 0.01 t}}{{(1 + e^{- 0.01 t})}^{2}}$ ، فأجد $C (t)$ .

$\begin{aligned} C (t) = \int C^{'} (t) d t = \int \frac{- 0.01 e^{- 0.01 t}}{{(1 + e^{- 0.01 t})}^{2}} d t \\ u = 1 + e^{- 0.01 t} \Rightarrow \frac{d u}{d t} = - 0.01 e^{- 0.01 t} \Rightarrow d t = \frac{d u}{- 0.01 e^{- 0.01 t}} \\ C (t) = \int \frac{- 0.01 e^{- 0.01 t}}{u^{2}} \times \frac{d u}{- 0.01 e^{- 0.01 t}} = \int u^{- 2} d u \\ = - u^{- 1} + K \end{aligned}$

(استعمل الرمز $K$ لثابت التكامل بدل $C$ المعتاد لتمييز ثابت التكامل عن رمز الاقتران $C$ ):

$\begin{aligned} C (t) = - {(1 + e^{- 0.01 t})}^{- 1} + K \\ C (0) = - (2)^{- 1} + K \\ \frac{1}{2} = - \frac{1}{2} \Rightarrow K = 1 \\ \Rightarrow C (t) = - {(1 + e^{- 0.01 t})}^{- 1} + 1 \\ C (t) = \frac{- 1}{1 + e^{- 0.01 t}} + 1 \end{aligned}$

(38) أجد قيمة $\int_{\ln 3}^{\ln 4} \frac{e^{4 x}}{e^{x} - 2} d x$ ، ثم اكتب الإجابة بالصيغة الآتية: $\frac{a}{b} + c \ln d$ ، حيث $a, b, c, d$ ثوابت صحيحة.

$\begin{aligned} u = e^{x} - 2 \Rightarrow \frac{d u}{d x} = e^{x} \Rightarrow d x = \frac{d u}{e^{x}} \\ e^{x} = u + 2 \\ x = \ln 3 \Rightarrow u = e^{\ln 3} - 2 = 3 - 2 = 1 \\ x = \ln 4 \Rightarrow u = e^{\ln 4} - 2 = 4 - 2 = 2 \\ \begin{aligned} \int_{\ln 3}^{\ln 4} \frac{e^{4 x}}{e^{x} - 2} d x & = \int_{1}^{2} \frac{e^{4 x}}{u} \frac{d u}{e^{x}} = \int_{1}^{2} \frac{e^{3 x}}{u} d u \\ = \int_{1}^{2} \frac{(u + 2)^{3}}{u} d u \\ = \int_{1}^{2} \frac{u^{3} + 6 u^{2} + 12 u + 8}{u} d u \\ = \int_{1}^{2} (u^{2} + 6 u + 12 + \frac{8}{u}) d u \end{aligned} \\ = {(\frac{1}{3} u^{3} + 3 u^{2} + 12 u + 8 \ln | u |) |}_{1}^{2} \end{aligned}$

(39) إذا كان: $f^{'} (x) = \tan x$ ، وكان: $f (3) = 5$ ، فأثبت أن $f (x) = \ln | \frac{\cos 3}{\cos x} | + 5$ .

$\begin{aligned} f (x) = \int \tan x d x = - \int \frac{- \sin x}{\cos x} d x = - \ln | \cos x | + C \\ f (3) = - \ln | \cos 3 | + C \\ 5 = - \ln | \cos 3 | + C \Rightarrow C = 5 + \ln | \cos 3 | \\ f (x) = - \ln | \cos x | + 5 + \ln | \cos 3 | = \ln | \frac{\cos 3}{\cos x} | + 5 \end{aligned}$

إعداد : شبكة منهاجي التعليمية

10 / 07 / 2023

حمّل تطبيق منهاجي الجديد

النقاشات

حمّل تطبيق منهاجي الجديد

النقاشات

جميع الحقوق محفوظة © 2025