أتدرب وأحل المسائل
الأعداد المركبة
أجد قيمة الجذر الرئيس في كلّ ممّا يأتي بدلالة i :
(1)
(2)
(3)
(4)
أجد ناتج كلّ ممّا يأتي في أبسط صورة مفترضاً أنّ :
(5) i26
(6) i39
(7)
(8)
(9)
(10)
أكتب في كلّ ممّا يأتي العدد المركب z بالصورة القياسية:
(11)
(12)
(13)
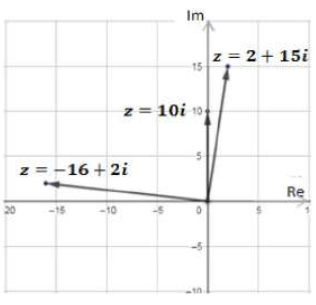
أحدد الجزء الحقيقي والجزء التخيلي لكلّ من الأعداد المركبة الآتية، ثم أمثلها جميعاً في المستوى المركب نفسه:
(14) z = 2 + 15i
(15) z = 10i
(16) z = -16 - 2i
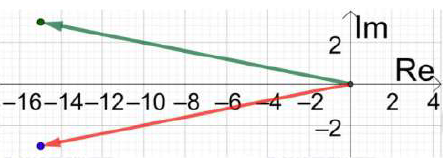
أمثل العدد المركب ومرافقه بيانياً في المستوى المركب في كل ممّا يأتي:
(17) z = -15 + 3i
= -15 – 3i
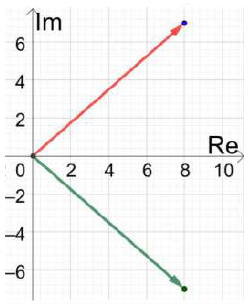
(18) z = 8 - 7i
= 8 + 7i
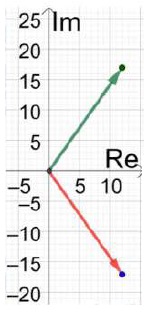
(19) z = 12 + 17i
= 12 – 17i
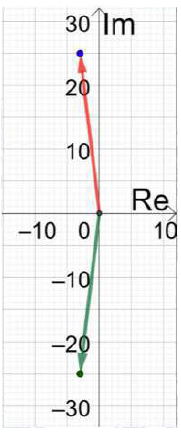
(20) z = -3 - 25i
= -3 + 25i
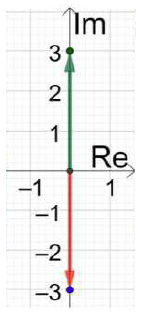
(21) 3i
= – 3i
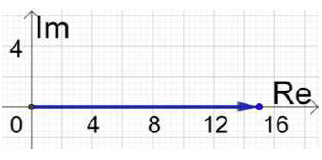
(22) 15
= 15
أجد لكل ممّا يأتي:
(23) z = -5 + 5i
(24) z = 3 - 3i
(25) z = 6 - 8i
إعداد : شبكة منهاجي التعليمية
10 / 07 / 2023
النقاشات