أستعد لدراسة الوحدة

المعدلات المرتبطة

حل المثلث باستعمال قانون جيوب التمام

أجد قيمة x في كلّ من المثلثات الآتية:

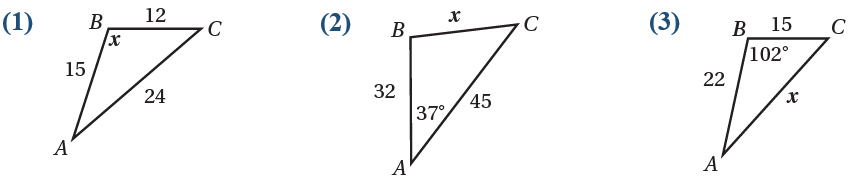
(1) 

$\begin{array}{rl}& {24}^2={12}^2+{15}^2-2\times 12\times 15cos x\\ & cos x=\frac{{12}^2+{15}^2-{24}^2}{2\times 12\times 15}=\frac{-207}{360} \to x\approx 2.18\mathrm{rad}\approx 125{.1}^{\circ }\end{array}$

(2)

$x^2={32}^2+{45}^2-2\times 32\times 45cos{37}^{\circ }\to x\approx 27.37$

(3)

$x^2={15}^2+{22}^2-2\times 15\times 22cos {102}^{\circ }\to x\approx 29.1$

حل المعادلات المثلثية

أحل كل معادلة ممّا يأتي في الفترة [0, 2π) :

(4) tan 2x + 1 = 0

$\begin{array}{rl}& tan 2x+1=0\to tan 2x=-1\to 2x=\frac{3\pi }{4},\frac{7\pi }{4},\frac{11\pi }{4},\frac{15\pi }{4}\\ & \to x=\frac{3\pi }{8},\frac{7\pi }{8},\frac{11\pi }{8},\frac{15\pi }{8}\end{array}$

(5) 2sin² x + sin x = 0

$\begin{array}{rl}2si{n}^2 x+sin x=0& \to sin x(2sin x+1)=0\\ & \to sin x=0 \text{or }sin x=-\frac{1}{2}\\ & \to x=0 , \pi ,\frac{7\pi }{6} , \frac{11\pi }{6}\end{array}$

(6) 1 – cos x = $\frac{1}{2}$

$1-cos x=\frac{1}{2}\to cos x=\frac{1}{2} \to x=\frac{\pi }{3},\frac{5\pi }{3}$

تحديد فترات التزايد وفترات التناقص

أحدد فترات التزايد وفترات التناقص لكل اقتران ممّا يأتي:

(7) f(x) = 6x² – 6x + 12

$\begin{array}{rl}& f^{\mathrm{\prime }}\left(x\right)=12x-6\\ & f^{\mathrm{\prime }}\left(x\right)=0\to x=\frac{1}{2}\end{array}$

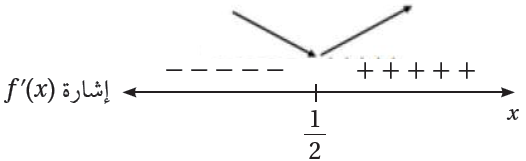
الاقتران f متناقص في ($\frac{1}{2}$-∞, ) ومتزايد في ($\frac{1}{2}$ , ∞).

(8) f(x) = x³ – 3x² + 4x + 3

$\begin{array}{rl}& f\left(x\right)=x^3-3x^2+4x+3\\ & f^{\mathrm{\prime }}\left(x\right)=3x^2-6x+4\\ & \mathrm{\Delta }=36-48=-12<0\end{array}$

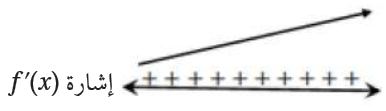
ليس للمشتقة أصفار وإشارتها مماثلة لإشارة معامل x² لجميع الأعداد الحقيقية؛ أي أنّ:

f ’ (x) > 0  ؛ فالاقتران متزايد على R

(9) f(x) = x² – 8x²

$\begin{array}{rl}& f\left(x\right)=x^2-8x^4\\ & f^{\mathrm{\prime }}\left(x\right)=2x-32x^3\\ & f^{\mathrm{\prime }}\left(x\right)=0\to 2x(1-16x^2)=0\\ & \to x=0 , x=\pm \frac{1}{4}\end{array}$

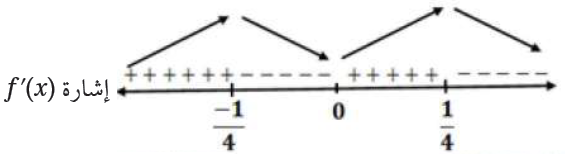
الاقتران f متزايد على (-∞ , $\frac{-1}{4}$) و (0$\frac{1}{4}$ , ).

الاقتران f متناقص على ($\frac{-1}{4}$, 0) و ($\frac{1}{4}$, ∞).