أتحقق من فهمي

أتحقق من فهمي

المستقيمات في الفضاء

توازي المتجهات

أتحقق من فهمي صفحة (127):

إذا كان: $G (7, 5, - 11), H (4, 4, - 4), K (4, 5, 3), L (7, 7, 3)$ ، فأحدد إن كان كل متجهين مما يأتي متوازيين أم لا:

$\vec{G H}, \vec{K L}$ (a)

$\begin{aligned} \vec{G H} = ⟨ - 3, - 1, 7 ⟩ \\ \vec{K L} = ⟨ 3, 2, 0 ⟩ \end{aligned}$

نلاحظ أنه لا يوجد عدد حقيقي $c$ يجعل العبارة $\vec{G H} = c (\vec{K L})$ صحيحة، ونستنتج أن $\vec{G H}, \vec{K L}$ غير متوازيين.

$\vec{G L}, \vec{H K}$ (b)

$\begin{aligned} \vec{G L} = ⟨ 0, 2, 14 ⟩ \\ \vec{H K} = ⟨ 0, 1, 7 ⟩ \end{aligned}$

نلاحظ أن $\vec{G L} = 2 \vec{H K}$ ، ونستنتج أن $\vec{G L} ∥ \vec{H K}$

أتحقق من فهمي صفحة (129):

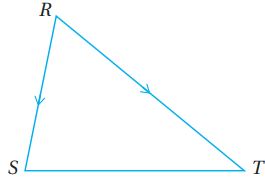
في المثلث RST المجاور، إذا كان: $\bar{R S} = 4 \vec{a}, \bar{R T} = 6 \vec{b}$ والنقطة U منتصف $\bar{R S}$ ، والنقطة V منتصف $\bar{R T}$ ، فأثبت أن $\vec{S T}$ يوازي $\vec{U V}$ .

$\begin{aligned} \vec{U V} & = \vec{U R} + \vec{R V} \\ = \frac{1}{2} (- 4 \vec{a}) + \frac{1}{2} (6 \vec{b}) = 3 \vec{b} - 2 \vec{a} \\ \vec{S T} & = \vec{S R} + \vec{R T} \\ = - 4 \vec{a} + 6 \vec{b} = 2 (3 \vec{b} - 2 \vec{a}) \end{aligned}$

إذن، $, \vec{S T} = 2 \vec{U V}$ ومنه المتجهان $\vec{S T}, \vec{U V}$ متوازيان.

أتحقق من فهمي صفحة (130):

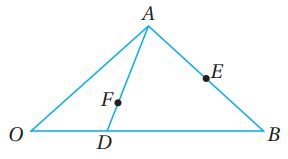
يظهر في الشكل المجاور المثلث OAB.

إذا كان: $\vec{O A} = \vec{a}, \vec{O B} = \vec{b}$ ، وكانت النقطة D تقع على $\bar{O B}$ ، والنقطة E منتصف $\bar{A B}$ ، والنقطة F تقع على $\bar{A D}$ ، حيث: $\vec{O F} = \frac{2}{5} (\vec{a} + \vec{b})$ ، فأثبت أن O، وF، وE تقع على استقامة واحدة.

$\begin{aligned} \vec{O F} = \frac{2}{5} (\vec{a} + \vec{b}) ⟹ \vec{a} + \vec{b} = \frac{5}{2} \vec{O F} \dots \dots \dots \dots \dots \dots (1) \\ \vec{O E} = \vec{O B} + \vec{B E} \\ = \vec{b} + \frac{1}{2} \vec{B A} \\ = \vec{b} + \frac{1}{2} (\vec{B O} + \vec{O A}) \\ = \vec{b} + \frac{1}{2} (- \vec{b} + \vec{a}) \\ = \frac{1}{2} (\vec{a} + \vec{b}) \\ \Rightarrow \vec{a} + \vec{b} = 2 \vec{O E} . . . . . . . . . . . . . . . . . . (2) \end{aligned}$

من العلاقتين (1) و(2) نستنتج أن:

$\frac{5}{2} \vec{O F} = 2 \vec{O E} \Rightarrow \vec{O F} = \frac{4}{5} \vec{O E}$

وهذا يعني أن المتجهين $\vec{O F}, \vec{O E}$ متوازيان، وبما أنهما ينطلقان من النقطة $O$ نفسها، إذن النقاط $O, E, F$ تقع على استقامة واحدة.

المعادلة المتجهة للمستقيم

أتحقق من فهمي صفحة (132):

أجد معادلة متجهة للمستقيم l الذي يوازي المتجه: $\vec{v} = ⟨ 1, - 4, - 5 ⟩$ ، ويمر بالنقطة $U (0, - 6, 9)$ .

$\begin{aligned} \vec{r} = {\vec{r}}_{0} + t \vec{v} \\ \vec{r} = ⟨ 0, - 6, 9 ⟩ + t ⟨ 1, - 4, - 5 ⟩ \end{aligned}$

أتحقق من فهمي صفحة (133):

أجد معادلة متجهة للمستقيم l المار بالنقطتين: $N (2, - 4, 3) g ، M (3, 7, - 9)$ .

$\begin{aligned} \vec{N M} = ⟨ 3 - 2, 7 - (- 4), - 9 - 3 ⟩ = ⟨ 1, 11, - 12 ⟩ \\ \vec{r} = {\vec{r}}_{0} + t \vec{v} \Rightarrow \vec{r} = ⟨ 3, 7, - 9 ⟩ + t ⟨ 1, 11, - 12 ⟩ \end{aligned}$

أتحقق من فهمي صفحة (136):

تمثل: $\vec{r} = 11 \hat{i} + 5 \hat{j} - 6 \hat{k} + t (7 \hat{i} - 2 \hat{j} + 5 \hat{k})$ معادلة متجهة للمستقيم l:

(a) أبين أن النقطة التي متجه الموقع لها هو $(39 \hat{i} - 3 \hat{j} + 14 \hat{k})$ تقع على المستقيم l.

$\vec{r} = (11 + 7 t) \hat{i} + (5 - 2 t) \hat{ȷ} + (- 6 + 5 t) \hat{k}$

نبحث عن قيمة ل $t$ تحقق:

$\begin{aligned} 39 \hat{i} - 3 \hat{ȷ} + 14 \hat{k} = (11 + 7 t) \hat{i} + (5 - 2 t) \hat{ȷ} + (- 6 + 5 t) \hat{k} \\ 39 = 11 + 7 t \Rightarrow t = 4 \\ - 3 = 5 - 2 t \Rightarrow t = 4 \\ 14 = - 6 + 5 t \Rightarrow t = 4 \end{aligned}$

بما أن للمعادلات الثلاث الحل نفسه $(t = 4)$ ، فإن القطة التي متجه موقعها $39 \hat{i} - 3 \hat{ȷ} + 14 \hat{k}$ وهي النقطة $(39, - 3, 14)$ تقع على المستقيم $l$ لأنها تنتج من تعويض $t = 4$ في معادلته.

(b) أجد متجه الموقع للنقطة التي تقع على هذا المستقيم، وتقابل القيمة: 3-= t.

$\begin{aligned} t = - 3 \Rightarrow & \vec{r} = (11 + 7 (- 3)) \hat{i} + (5 - 2 (- 3)) \hat{ȷ} + (- 6 + 5 (- 3)) \hat{k} \\ = - 10 \hat{i} + 11 \hat{ȷ} - 21 \hat{k} \end{aligned}$

(c) إذا كانت النقطة $(v, - 3 v, 5 v - 1)$ تقع على المستقيم l، فما قيمة v؟

متجه الموقع للنقطة $v \hat{ı} - 3 v \hat{ȷ} + (5 v - 1) \hat{k} ه (v, - 3 v, 5 v - 1) \hat{2}$

$\begin{aligned} v \hat{i} - 3 v \hat{ȷ} + (5 v - 1) \hat{k} = (11 + 7 t) \hat{1} + (5 - 2 t) \hat{ȷ} + (- 6 + 5 t) \hat{k} \\ v = 11 + 7 t \dots \dots \dots \dots (1) \\ - 3 v = 5 - 2 t \dots \dots \dots (2) \\ 5 v - 1 = - 6 + 5 t \dots \dots (3) \\ (1) \times 3 + (2) \Rightarrow 0 = 38 + 19 t \\ \Rightarrow t = - 2 \\ \Rightarrow v = - 3 \end{aligned}$

تتحقق من أن $v = - 3, t = - 2$ تحققان المعادلة (3)

$\begin{matrix} 5 (- 3) - 1 = - 6 + 5 (- 2) \\ - 16 = - 16 \end{matrix}$

إذن، قيمة $v$ التي تجعل النقطة $(v, - 3 v, 5 v - 1)$ واقعة على المستقيم $l$ هي: $v = - 3$

المستقيمات المتوازية والمتقاطعة والمتخالفة

أتحقق من فهمي صفحة (136):

إذا كانت: $\vec{r} = ⟨ 3, 7, - 9 ⟩ + t ⟨ 1, 11, - 12 ⟩$ معادلة متجهة للمستقيم $l_{1}$ ، وكانت: $\vec{r} = ⟨ - 30, - 6, 30 ⟩ + u ⟨ 4, - 6, 3 ⟩$ معادلة متجهة للمستقيم $l_{2}$ ، ، فأحدد إذا كان المستقيمان: $l_{2}, l_{1}$ متوازيين، أو متقاطعين، أو متخالفين، ثم أجد إحداثيات نقطة تقاطعهما إذا كانا متقاطعين.

اتجاه المستقيم $l_{1}$ هو ${\vec{v}}_{1} = ⟨ 1, 11, - 12 ⟩$

اتجاه المستقيم $l_{2}$ هو ${\vec{v}}_{2} = ⟨ 4, - 6, 3 ⟩$

وبما أنه لا يوجد عدد حقيقي k بحيث ${\vec{v}}_{1} = k {\vec{v}}_{2}$ فإن المستقيمين غير متوازيين.

نساوي $\vec{r}$ من معادلتي المستقيمين:

$\begin{aligned} ⟨ 3, 7, - 9 ⟩ + t ⟨ 1, 11, - 12 ⟩ = ⟨ - 30, - 6, 30 ⟩ + u ⟨ 4, - 6, 3 ⟩ \\ 3 + t = - 30 + 4 u \Rightarrow t - 4 u = - 33 \dots \dots \dots \dots \dots (1) \\ 7 + 11 t = - 6 - 6 u \Rightarrow 11 t + 6 u = - 13 \dots \dots \dots \dots (2) \\ - 9 - 12 t = 30 + 3 u \Rightarrow 12 t + 3 u = - 39 \dots \dots \dots \dots (3) \\ 3 \times (1) + 2 \times (2) \Rightarrow 25 t = - 125 \Rightarrow t = - 5, u = 7 \end{aligned}$

نتحقق من أن $u = 7, t = - 5$ تحققان المعادلة (3)

$\begin{aligned} 12 (- 5) + 3 (7) \overset{?}{=} - 39 \\ - 39 = - 39 \end{aligned}$

بما أن قيمة $t$ وقيمة $u$ حققتا المعادلات الثلاث، فإن المستقيمين متقاطعان.

لإيجاد إحداثيات نقطة التقاطع نعوض $t = - 5$ في معادلة $l_{1}$ :

$\vec{r} = ⟨ 3, 7, - 9 ⟩ - 5 ⟨ 1, 11, - 12 ⟩ = ⟨ - 2, - 48, 51 ⟩$

إذن، يتقاطع المستقيمان في النقطة $(- 2, - 48, 51)$

أتحقق من فهمي صفحة (138):

عرض جوي: أقلعت طائرة من موقع إحداثياته: $(0, 7, 0)$ . وفي الوقت نفسه، أقلعت طائرة ثانية من موقع إحداثياته: $(- 2, 0, 0)$ . وبعد التحليق مدة قصيرة في مسارين مستقيمين، أصبحت الطائرة الأولى عند الموقع الذي إحداثياته: $(8, 15, 16)$ ، وأصبحت الطائرة الثانية عند الموقع الذي إحداثياته: $(22, 24, 48)$ . هل خطا سير الطائرتين متوازيان، أم متقاطعان، أم متخالفان؟

اتجاه الطائرة الأولى هو اتجاه الطائرة الأولى هو ${\vec{v}}_{1} = ⟨ 8 - 0, 15 - 7, 16 - 0 ⟩ = ⟨ 8, 8, 16 ⟩$

ويمكن تبسيطه بالقسسة على 8 ليصبح: $⟨ 1, 1, 2 ⟩$

معادلة مسار الأولى: $\vec{r} = ⟨ 0, 7, 0 ⟩ + t ⟨ 1, 1, 2 ⟩$

اتجاه الثانية هو ${\vec{v}}_{2} = ⟨ 22 - (- 2), 24 - 0, 48 - 0 ⟩ = ⟨ 24, 24, 48 ⟩$

ويمكن تبسيطه بالقسمة على 24 دون تغيير اتجاهه ليصبح: $⟨ 1, 1, 2 ⟩$

معادلة مسار الثانية: $\vec{r} = ⟨ - 2, 0, 0 ⟩ + u ⟨ 1, 1, 2 ⟩$

نلاحظ أن المسارين متوازيان لأن لهما الاتجاه نفسه.

إعداد : شبكة منهاجي التعليمية

15 / 02 / 2023

النقاشات

جميع الحقوق محفوظة © 2024