إجابات مراجعة الدرس الثاني
دارات التيار الكهربائي المتردد
السؤال الأول:
الفكرة الرئيسة: أوضح المقصود بكل من؛ المعاوقة المحثية والمعاوقة المواسعية، وأبين العوامل التي تؤثر في كل منهما.
المعاوقة المحثية: الممانعة التي يبديها المحث الموصول في دارة كهربائية مغلقة لمرور تيار كهربائي متردد فيها. وتعتمد على محاثة المحث (تتناسب طردياً)، وعلى التردد الزاوي لمصدر فرق الجهد في الدارة (تتناسب طردياً).
المعاوقة المواسعية: الممانعة التي يبديها المواسع الموصول في دارة كهربائية لمرور تيار كهربائي متردد فيها. وتعتمد على مواسعة المواسع (تتناسب عكسياً)، وعلى التردد الزاوي لمصدر فرق الجهد في الدارة (تتناسب عكسياً).
السؤال الثاني:
أوضح المقصود بالقيمة العظمى والقيمة الفعالة لفرق الجهد المتردد.
القيمة العظمى لفرق الجهد المتردد: سعة الاقتران الموجي لفرق الجهد المتردد، وهي أكبر قيمة لفرق الجهد بين طرفي المصدر.
القيمة الفعالة لفرق الجهد المتردد: الجذر التربيعي للقيمة المتوسطة لمربعات قيم الجهد المتردد.
السؤال الثالث:
تفكير ناقد: أوضح لماذا ينعدم التيار المتردد في دارة (AC) تحتوي على مواسع فقط عند الترددات المخفضة جداً. وأوضّح لماذا ينعدم التيار في دارة (AC) تحتوي على محث فقط عند الترددات العالية جداً.
في دارة التيار المتردد التي تحتوي على مواسع فقط، ينعدم التيار عند الترددات المخفضة جداً لفرق الجهد المتردد؛ لأنه بانخفاض التردد تزداد المعاوقة المواسعية، حيث تتناسب معاوقة المواسع عكسياً مع تردد فرق الجهد.
في دارة التيار المتردد التي تحتوي على محث فقط، ينعدم التيار عند الترددات المرتفعة جداً لفرق الجهد المتردد؛ لأنه بارتفاع التردد تزداد المعاوقة المحثية، حيث تتناسب معاوقة المحث طردياً مع تردد فرق الجهد.
السؤال الرابع:
أفسر: عند مضاعفة تردد مصدر فرق الجهد إلى مثليه، في دارة تيار متردد تحتوي (RLC)، على نحو ما هو مبين في الشكل، ماذا يحدث لكل من: R, XL, XC ؟
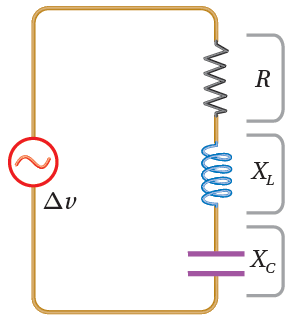
- المقاومة (R) لا تتغير.
- المعاوقة المواسعية (XL) تنخفض إلى النصف.
- المعاوقة المحثية (XC) تتضاعف إلى مثليها.
السؤال الخامس:
أستخدم المتغيرات: ما القيمة العظمى للتيار المتردد في دارة (AC)، تحتوي على مواسع مواسعته ، ومصدر فرق جهد قيمته العظمى (111 V) وتردده (86 Hz)؟
السؤال السادس:
أحسب: عند أي تردد زاوي تتساوى المعاوقة المحاثية لمحث مع المعاوقة المواسعية لمواسع في دارة تيار متردد؟ وماذا يُسمى هذا التردد؟
يُسمى هذا التردد بتردد الرنين.
السؤال السابع:
أستخدم المتغيرات: دارة (RLC) تتكون من مقاومة () ومواسع ، ومحث، موصولة على التوالي بمصدر فرق جهد متردد، جهده الفعال (12 V) ، وتردده الزاوي (2000 rad/s). أجد محاثة المحث التي تجعل للتيار الفعال أكبر قيمة، ثم أجد أكبر قيمة للتيار الفعال.
إعداد : شبكة منهاجي التعليمية
27 / 01 / 2023
النقاشات