فكرة الدرس:
تعرُّفُ مفهومِ الاقترانِ المُركَّبِ، وشرطِ تركيبِ اقترانيْنِ، وإيجادُ قيمتِهِ لعددٍ مُعطى، وإيجادُ قاعدةِ اقترانٍ مُركَّبٍ إذا عُلِمَتْ قاعدتا مُركَّبتيْهِ.
تعلَّمْتُ سابقًا أنَّهُ يُمكِنُ استعمالُ أيِّ اقترانيْنِ، مثلِ f(x) = x2 , g(x) = 2x -1 ، لتكوينِ اقتراناتٍ جديدةٍ، وذلكَ بإجراءِ عملياتِ جمعٍ، أوْ طرحٍ، أوْ ضربٍ، أوْ قسمةٍ عليْهِما كما في الأمثلةِ الآ تيةِ:
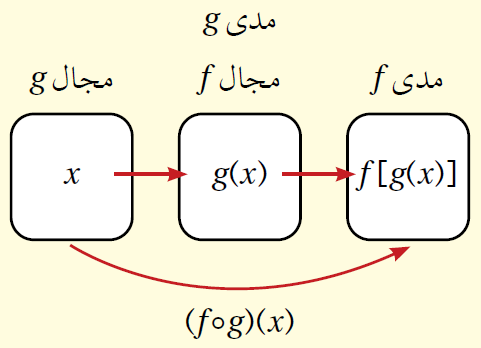
ويمكنُ أيضًا تكوينُ اقترانٍ جديدٍ منَ الاقترانيْنِ f، وَ g عنْ طريقِ دمجِهِما، بحيثُ تكونُ مخرجةُ أحدهِما مدخلةً للآخرِ.
وتُسمّى عمليةُ الدمجِ هذهِ تركيبَ الاقتراناتِ ( functions composition )، ويُسمّى الاقترانُ الناتجُ الاقترانَ المُركَّبَ (composite function).
يُمكِنُ تركيبُ الاقترانيْنِ ( f(x), g(x بطريقتيْنِ، هما:
1) تطبيقُ g أولً، ثمَّ تطبيقُ f على نتيجةِ g، ويُرمَزُ إلى ذلكَ بالرمزِ
2) تطبيقُ f أولً، ثمَّ تطبيقُ g على نتيجةِ f، ويُرمَزُ إلى ذلكَ بالرمزِ
مفهوم أساسي: تركيبُ الاقتراناتِ
إذا كانَ (f(x و (g(x اقترانينِ، وكانَ مدى g(x) يقعُ ضمنَ مجالِ (f(x فإنَّ الاقترانَ المُركّبَ يُعطى كما يأتي:
إعداد : شبكة منهاجي التعليمية
24 / 04 / 2022
النقاشات