المجال الكهربائي المنتظم
U n i f o r m E l e c t r i c F i e l d
يعد المجال الكهربائي الناشئ عن الشحنات النقطية مجالًا كهربائيًّا غير منتظم، فكيف يمكن الحصول على مجال كهربائي منتظم؟ وكيف نعبر عنه ريا ضيًّا؟
عند شحن صفيحتين موصلتين متوازيتين إحداهما بشحنة سالبة والأخرى بشحنة موجبة كما يبين الشكل:
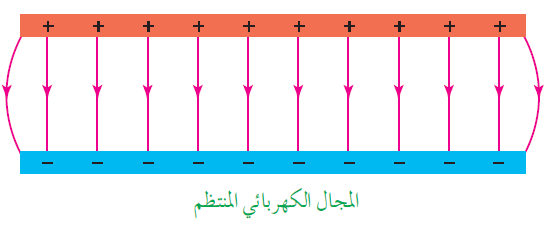
فإن الشحنة تتوزع على سطحيهما بانتظام، وينشأ مجال كهربائي منتظم ثابت مقدارًا واتجاهًا عند النقاط جميعها في الحيز بين الصفيحتين وبعيدًا عن الأطراف. ويمثَّل المجال الكهربائي المنتظم بخطوط مستقيمة متوازية والبعد بينها متساوٍ ، اتجاهها يمثل اتجاه المجال الكهربائي، وكثافتها تعبّر عن مقداره.
لاحظ أن مصدر المجال الكهربائي في هذه الحالة الحالة الشحنات الموزعة على سطحي الصفيحتين. وتسمى كثافة الشحنة هنا بالكثافة السطحية للشحنة ويرمز لها بالرمز σ .
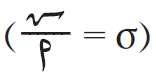
من العلاقة السابقة نستنتج:
- الكثافة السطحية للشحنة تعرف بإنها كمية الشحنة الكهربائية لكل وحدة مساحة.
- تقاس بوحدة كولوم/م 2
- تعتمد على عاملين: مقدارالشحنة على إحدى الصفيحتين، ومساحة الصفيحة.
يتناسب مقدار المجال الكهربائي المنتظم طرديًّا مع الكثافة السطحية للشحنة على الصفيحتين، ويعتمد المجال الكهربائي أيضا على السماحية الكهربائية للوسط الفاصل بين الصفيحتين، فإذا كانت الكثافة السطحية للشحنة على الصفيحتين متساوية، وكان الوسط بين الصفيحتين هواءً أو فراغًا فإن المجال الكهربائي المنتظم يعطى بالعلاقة الرياضية الآتية:
العوامل المؤثرة للمجال الكهربائي المنتظم
من العلاقة السابقة نستنتج، أن مقدار المجال الكهربائي المنتظم يعتمد على:
- مقدار الشحنة على إحدى الصفيحتين.
- مساحة الصفيحة.
- الكثافة السطحية للشحنة (طرديًّا).
- السماحية الكهربائية للوسط الفاصل بين الصفيحتين.
حركة جسيم مشحون في مجال كهربائي منتظم
عندما يوضع جسيم مشحون كتلته (ك) في مجال كهربائي منتظم فإنه يتأثر بقوة كهربائية ثابتة مقدارًا واتجاهًا. فإذا تحرك الجسيم تحت تأثير هذه القوة فإنه سيكتسب تسارعًا (ت) ثابتًا مقدارًا واتجاهًا، وفقًا للقانون الثاني لنيوتن. وفي حالة الجسيمات الذرية (البروتونات والإلكترونات) فإن وزنها يكون مهملاً مقارنة بالقوة الكهربائية المؤثرة فيها؛ لذلك فإن القوة الكهربائية تمثل ق المحصلة، أي أن:
ق محصلة = ك ت
ق ك = ك ت
مـ ش = ك ت
وبذلك فإن التسارع:

استنتج من العلاقة السابقة العوامل التي يعتمد عليها التسارع؟
- ..........................................
- ..........................................
- ..........................................
معادلات الحركة بتسارع ثابت:
بما أن التسارع ثابت فإن حركة الجسيم يمكن وصفها باستخدام معادلات الحركة بتسارع ثابت:

عند التعويض في معادلات الحركة السابقة:
(ت +): ع2 < ع1
(ت -): ع2 > ع1
مثال ( 1- 5):
صفيحتان موصلتان متوازيتان مساحة كل منهما (1 × 10-2) م2، شحنت إحداهما بشحنة موجبة والأخرى بشحنة سالبة، وكانت الشحنة الكهربائية على كل صفيحة (1,77 × 10-9) كولوم. إذا علمت أن (ₒε = 8,85 х 10–12) كولوم2/نيوتن . م2 . فاحسب مقدار:
- المجال الكهربائي في الحيز بين الصفيحتين.
- القوة الكهربائية المؤثرة في شحنة (1 × 10–9) كولوم توضع في الحيز بين الصفيحتين.
- المجال الكهربائي عندما تصبح الشحنة الكهربائية ضعفي ما كانت عليه على كل من الصفيحتين، مع بقاء مساحة كل من الصفيحتين ثابتة.
إعداد : أ. مصطفى دعمس
21 / 07 / 2019
النقاشات