أتدرب وأحل المسائل
حالات خاصة من التحليل
أحلل كلاً مما يأتي:
1) u2 - 64
(u - 8)(u + 8)
2) x2 -
(x - )(x + )
3) 36y2 -1
(6y - 1)(6y + 1)
4) v4 – 625r2
(v2 – 25r)(v2 + 25r)
5) a2 – w2z2
(a - wz)(a + wz)
6) -16y2 + 49
(7 – 4y)(7 + 4y)
أحلل كلاً مما يأتي:
7) ab2 – 100a
a(b - 10)(b + 10)
8) x – x3
x(1 - x)(1 + x)
9) 12b3 + 2b2 – 192b - 32
2(6b + 1)(b - 4)(b + 4)
10) d3 – 5d2 – 100d + 500
(d - 5)(d - 10)(d + 10)
أحدد أن كل ثلاثية حدود ممّا يأتي تمثل مربعًا كاملًا أَم لا، وإذا كانت تمثله فأحللها:
11) w2 – 18w + 81
(w - 9)2 مربع كامل
12) x2 + 2x - 1
ليس مربعاً كاملاً
13) y2 + 8y + 16
(y + 4)2 مربع كامل
14) 9x2 – 30x + 10
ليس مربعاً كاملاً
أحلل كلاً مما يأتي:
15) 3t3 + 24t2 + 48t
3t(t + 4)2
16) 50g2 + 40g + 8
2(5g + 2)2
17) 27g2 – 90g + 75
2(3g - 5)2
18) 18y2 – 48y + 32
2(3y - 4)2
19) 5x2 – 60x + 180
5(x – 6)2
20) 16r3 – 48r2 + 36r
4r(2r – 3)2
21) 12x2 – 84x + 147
3(2x – 7)2
22) 4x2 – 80x + 400
4(x – 10)2
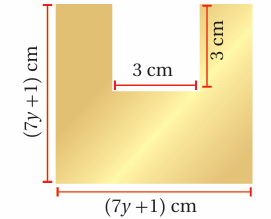 (23) نحاس: يبين الشكل المجاور صفيحة من النحاس قبل صهرها وتحويلها إلى مستطيل له المساحة نفسها، أجد قياسين ممكنين لطول المستطيل وعرضه بدلالة y .
(23) نحاس: يبين الشكل المجاور صفيحة من النحاس قبل صهرها وتحويلها إلى مستطيل له المساحة نفسها، أجد قياسين ممكنين لطول المستطيل وعرضه بدلالة y .
(7y – 2), (7y + 4)
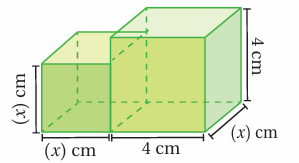 (24) يبين الشكل المجاور مخططاً لمستودعي تخزين متجاورين. أكتب مقدارًا جبريًا يمثل الفرق بين حجمي المستودعين، ثم أَحلله.
(24) يبين الشكل المجاور مخططاً لمستودعي تخزين متجاورين. أكتب مقدارًا جبريًا يمثل الفرق بين حجمي المستودعين، ثم أَحلله.
x(4 – x)(4 + x)
إعداد : شبكة منهاجي التعليمية
26 / 10 / 2024
النقاشات