أتدرب وأحل المسائل

أتدرب وأحل المسائل

الاقتران التربيعي

أجد إحداثيي الرأس ومعادلة محور التماثل، والقيمة العظمى أو الصغرى ومجال كل من الاقترانات التربيعية الآتية ومداها:

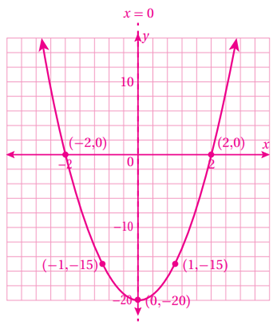
1) f(x) = 3x²

الرأس	المعادلة	عظمى /صغرى	المجال	المدى
(0, 0)	x = 0	صغرى : 0	(-∞,∞)	[0, ∞)

2) f(x) = $\frac{1}{2}$ x²

الرأس	المعادلة	عظمى /صغرى	المجال	المدى
(0, 0)	x = 0	صغرى : 0	(-∞,∞)	[0, ∞)

3) f(x) = -x² + 5

الرأس	المعادلة	عظمى /صغرى	المجال	المدى
(0, 5)	x = 0	عظمى : 5	(-∞,∞)	(-∞, 5]

4) f(x) = x² + 3

الرأس	المعادلة	عظمى /صغرى	المجال	المدى
(0, 3)	x = 0	صغرى : 3	(-∞,∞)	[3, ∞)

5) f(x) = 3x² + 6x - 2

الرأس	المعادلة	عظمى /صغرى	المجال	المدى
(-1, -5)	x = -1	صغرى : -5	(-∞,∞)	[-5, ∞)

6) f(x) = -8x + 2x²

الرأس	المعادلة	عظمى /صغرى	المجال	المدى
(2, -8)	x = 2	صغرى : -8	(-∞,∞)	[-8, ∞)

7) f(x) = -2x² - 6x + 4

الرأس	المعادلة	عظمى /صغرى	المجال	المدى
(- $\frac{17}{2}$ , $\frac{3}{2}$ )	x = -3	عظمى : $\frac{17}{2}$	(-∞,∞)	(-∞, $\frac{17}{2}$ ]

8) f(x) = 5 + 16x -2x²

الرأس	المعادلة	عظمى /صغرى	المجال	المدى
(4, 37)	x = 4	عظمى : 37	(-∞,∞)	(-∞, 37]

9) f(x) = -2(x – 4)² -3

الرأس	المعادلة	عظمى /صغرى	المجال	المدى
(4, -3)	x = 4	عظمى : -3	(-∞,∞)	(-∞, 3]

أجد إحداثتي الرأس ومعادلة محور التماثل، والقيمة العظمى أو الصغرى ومجال كل من القطوع المكافئة الآتية ومداها:

10)

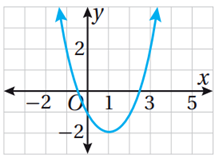
الرأس	المعادلة	عظمى /صغرى	المجال	المدى
(1, -2)	x = 1	صغرى : -2	(-∞,∞)	[-2, ∞)

11)

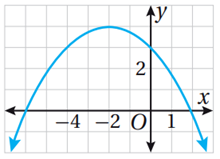
الرأس	المعادلة	عظمى /صغرى	المجال	المدى
(-2, 4)	x = 1	عظمى : 4	(-∞,∞)	(-∞, 4]

12)

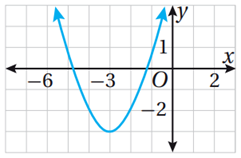
الرأس	المعادلة	عظمى /صغرى	المجال	المدى
(-3, -3)	x = 1	صغرى : -3	(-∞,∞)	[-3, ∞)

أمثل كلاً من الاقترانات الآتية بيانياً:

13) f(x) = x² + 6x - 2

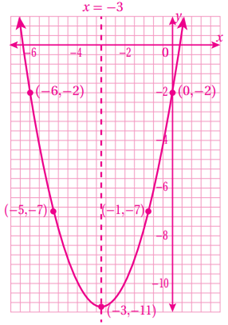
14) f(x) = 2x² – 10x + 1

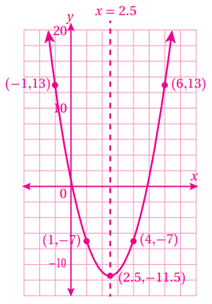
15) f(x) = -3x² + 18x + 6

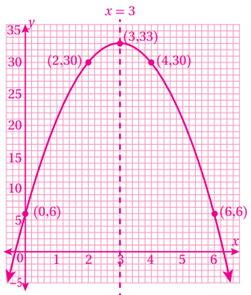
16) f(x) = -4x² - 8x + 7

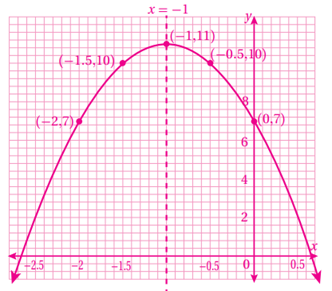
17) f(x) = - $\frac{1}{2}$ x² + 4x - 6

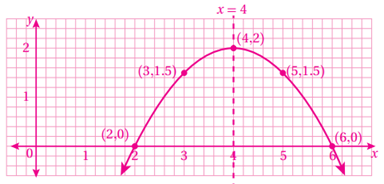
18) f(x) = 5x² - 20

19) 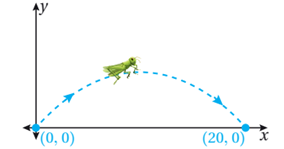حشرات: يمثل الاقتران f(x) = - $\frac{1}{20}$ x² + x ارتفاع جندب بالسنتيمتر فوق سطح الأرض عند قفزه؛ حيث x المسافة الأفقيَّة من نقطة القفز. أجد أقصى ارتفاع يمكن أن يصل إليه الجندب.

f(10) = 5 cm

رياضة: يمثل الاقتران h(t) = -4.9t² + 3.8t + 0.5 ارتفاع كرة مضرب بالأمتار فوق سطح الأرض، بعد t ثانية من ضرب سمير لها.

20) أجد ارتفاع الكرة لحظة ضرب سمير لها.

h(0) = 0.5 cm

21) أَجد أقصى ارتفاع يمكن أن تصل إليه الكرة.

f(0.4) ≈ 1.24 m