طباعة الدرس

أتدرب وأحل المسائل

الاقترانات

أحدد مجال كل علاقة مما يأتي ومداها، ثم أحدد ما إذا كانت تمثل اقتراناً أم لا:

1)

المجال: {-2, 1, 4}

المدى: {-3, 1, 2, 3}

ليس اقتراناً، 1 من المجال ارتبط مع -3 و 1 من المدى.

2)

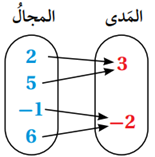
المجال: {-1, 2, 5, 6}

المدى: {-2, 3}

اقتران.

3)

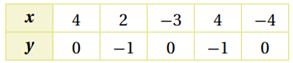
المجال: {-4, -3, 2, 4}

المدى: {0, -1}

ليس اقتراناً، 4 من المجال ارتبط مع -1 و 0 من المدى.

4)

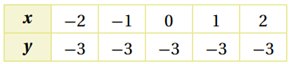
المجال: {-2, -1, 0, 1, 2}

المدى: {-3}

اقتران.

5) {(-2, 5), (-1, 2), (0, 4), (1, -9)}

المجال: {-2, -1, 0, 1}

المدى: {-9, 2, 4, 5}

اقتران.

6) {(4, 2), (1, 1), (0, 0), (1, -1), (4, -2)}

المجال: {0, 1, 4}

المدى: {-2, -1, 0, 1, 2}

ليس اقتراناً، 4 من المجال ارتبط مع -2 و 2 من المدى.

أحدد ما إذا كان كل اقتران مما يأتي منفصلاً أم متصلاً، ثم أحدد مجاله ومداه:

7)

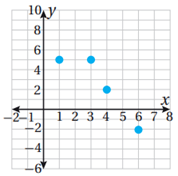
منفصل.

المجال: {1, 3, 4, 6}

المدى: {-2, 2, 5}

8)

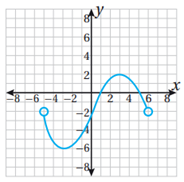
متصل.

المجال: {-5, 6}

المدى: {-6, 2}

9)

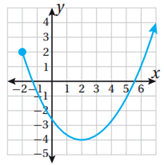
متصل.

المجال: {-2, ∞}

المدى: {-4, ∞}

10)

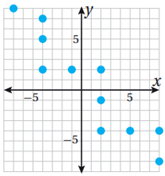
ليس اقتراناً، -4 من المجال ارتبط مع 2 و 5 و 7 من المدى.

11)

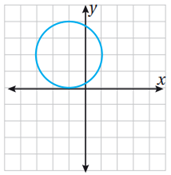
ليس اقتراناً ، كل من -2 و -1 و 0 من المجال ارتبط بعنصرين من المدى.

12)

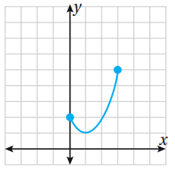
اقتران؛ لأنه ينجح في اختبار الخط الرأسي.

إذا كان f(x) = 3x - 8 فأَجد:

13) f(-3)

-17

14) 2f(-5) - 11

3

15) قيمة x، التي تجعل f(x) = 19

9

إذا كان h(x) = $\frac{x + 1}{x - 1}$، فأجد كلاً مما يأتي:

16) h(2)

3

17) h(3)

2

18) 2h(0) – h(-2)

-2$\frac{1}{3}$

تغذية: يمثل الاقتران 98c = (c)V عدد وحدات فيتامين د، التي يمكن للإنسان أن يحصل عليها عند شربه c كوبًا من الحليب:

19) أجد عدد وحدات فيتامين د، التي يمكن للإنسان أن يحصل عليها عند شرب 8 أكواب من الحليب.

784

20) إذا كان الحد الأقصى لعدد أكواب الحليب التي يوصي الأطباء المرأة الحامل أن تشربها 4 أكواب، فأجد مجال الاقتران ومداه.

المجال: [0, 4]، المدى: [0, 392]