طباعة الدرس

مهارات التفكير العليا

المعدلات المرتبطة

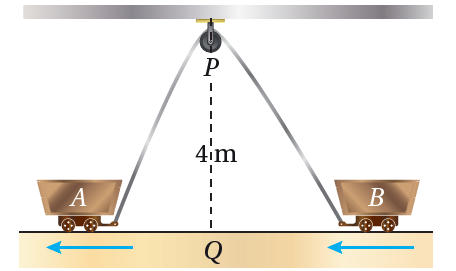(28) تبرير: رُبطت العربتان A و B بحبل طوله 12 m ، وهو يمر بالبكرة P كما في الشكل المجاور. إذا كانت النقطة Q تقع على الأرض بين العربتين أسفل P مباشرة، وتبعد عنها مسافة 4 m ، وكانت العربة A تتحرك بعيداً عن النقطة Q بسرعة 0.5 m/s ، فأجد سرعة اقتراب العربة B من النقطة Q في اللحظة التي تكون فيها العربة A على بُعد 3 m من النقطة Q ، مبرراً إجابتي.

لتكن الأبعاد كما في الشكل أدناه:

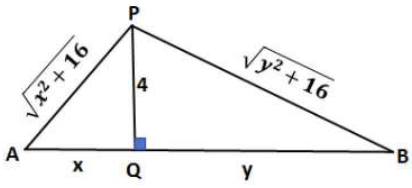
المعطى:

$\frac{dx}{dt}=0.5\mathrm{m}/\mathrm{s}$

المطلوب:

${\frac{dy}{dt}|}_{x=3}$

طول الحبل:

$AP+BP=\sqrt{x^2+16}+\sqrt{y^2+16}=12$

عندما x = 3 فإن:

$\begin{array}{rl}& \sqrt{9+16}+\sqrt{y^2+16}=12\to \sqrt{y^2+16}=7\to y=\sqrt{33}\\ & \sqrt{x^2+16}+\sqrt{y^2+16}=12\\ & \frac{x\frac{dx}{dt}}{\sqrt{x^2+16}}+\frac{y\frac{dy}{dt}}{\sqrt{y^2+16}}=0\\ & \frac{dy}{dt}=-\frac{x\sqrt{y^2+16}}{y\sqrt{x^2+16}}\frac{dt}{dt}\\ & {\frac{dy}{dt}|}_{x=3}=-\frac{3\sqrt{33+16}}{\sqrt{33}\sqrt{25}}\times 0.5=-\frac{21}{10\sqrt{33}}\mathrm{m}/\mathrm{s}\end{array}$

إذن، تقترب العربة B من النقطة Q بسرعة مقدارها $\frac{21}{10\sqrt{33}}\mathrm{m}/\mathrm{s}$

 

(29) تبرير: يركض عداء في مضمار دائري، طول نصف قطره 100 m ، بسرعة ثابتة مقدارها 7 m/s ، ويقف عداء آخر على بعد 200 m من مركز مضمار الركض. أجد معدل تغير المسافة بين العداءين عندما تكون المسافة بينهما 200 m .

تنبيه: أجد جميع الحلول الممكنة.

ليكن العداء الأول A والعداء الثاني B والبعد بينهما x كما في الشكل، وليكن L هو طول القوس الأصغر AD . توجد حالتان لموقع العداء A كما في الرسم الآتي:

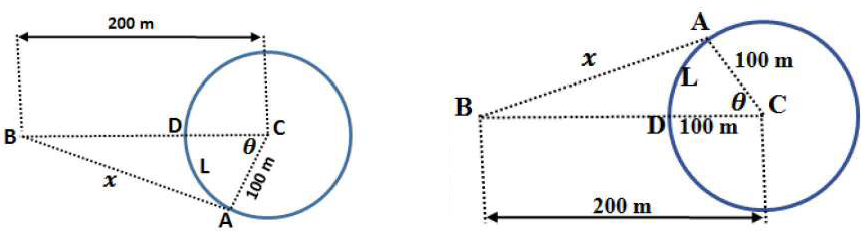
الحالة الأولى: العداء A إلى يمين B

المعطى: (لتكن L متناقصة)، ويكون:

$\frac{dL}{dt}=-7\mathrm{m}/\mathrm{s}$

المطلوب:

${\frac{dx}{dt}|}_{x=200\mathrm{m}}$

$\begin{array}{rl}& \begin{array}{rl}& L=r\theta =100\theta \to \frac{dL}{dt}=100\frac{d\theta }{dt}\end{array}\\ & \to \frac{d\mathit{\theta }}{d\mathit{t}}=-\mathbf{0}.07\mathrm{rad}/\mathrm{s}\\ & x^2=(200{)}^2+(100{)}^2-2\left(200\right)\left(100\right)cos\theta \\ & x^2=50000-40000cos\theta \\ & 2x\frac{dx}{dt}=40000sin\theta \frac{d\theta }{dt}\\ & \frac{dx}{dt}=\frac{20000sin\theta }{x}\frac{d\theta }{dt}\\ & cos\theta =\frac{50000-x^2}{40000}\end{array}$

عندما x = 200 فإن:

$cos\theta =\frac{50000-40000}{40000}=\frac{1}{4}$

ومنه:

$\begin{array}{rl}& sin\theta =\frac{\sqrt{15}}{4}\\ & {\frac{dx}{dt}|}_{x=200}=\frac{20000\frac{\sqrt{15}}{4}}{200}\times -0.07=-\frac{7\sqrt{15}}{4}\mathrm{m}/\mathrm{s}\end{array}$

الحالة الثانية: العداء A إلى يسار B

عندئذ يتزايد طول القوس L ، ويكون $\frac{dL}{dt}=7$، ويكون $\frac{d\theta }{dt}=0.07\mathrm{rad}/\mathrm{s}$ ، وعليه فإن:

${\frac{dx}{dt}|}_{x=200}=\frac{20000\frac{\sqrt{15}}{4}}{200}\times 0.07=\frac{7\sqrt{15}}{4}\mathrm{m}/\mathrm{s}$

إذن، عندما تكون المسافة بين العدائين 200 m ، فإنهما يقتربان من بعضهما أو يتباعدان عن بعضهما بسرعة مقدارها $\frac{7\sqrt{15}}{4}\mathrm{m}/\mathrm{s}$

 

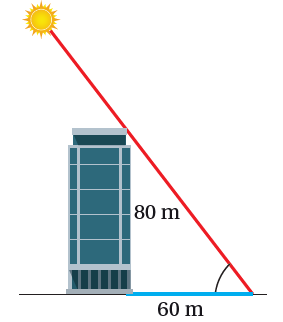 (30) تحدّ: سطعت الشمس في أحد الأيام فوق مبنى ارتفاعه 80 m ، فكان طول ظلّ المبنى في هذه اللحظة 60 m كما في الشكل المجاور. أجد معدل تغير طول ظل المبنى في هذه اللحظة بوحدة cm/min ، مقرباً إجابتي إلى أقرب جزء من عشرة، علماً بأنّ الشمس في هذا اليوم ستمر فوق المبنى تماماً.

إرشاد: تُكمل الأرض دورة كاملة حول نفسها كل 24 ساعة.

ليكن طول ظل المبنى x ، وزاوية ارتفاع الشمس Ɵ .

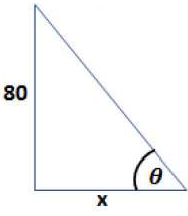
الشمس في هذا اليوم ستمر فوق المبنى تماماً، يعني أن الزاوية Ɵ متزايدة.

المعطى:

$\frac{d\theta }{dt}=\frac{2\pi \mathrm{rad}}{24h}=\frac{\pi }{12}\frac{\mathrm{rad}}{h}=\frac{\pi \mathrm{rad}}{12\times 60\min }=\frac{\pi }{720}\mathrm{rad}/\min$

المطلوب:

${\frac{dx}{dt}|}_{x=60}$

العلاقة التي تربط المتغيرين هي:

$\begin{array}{rl}tan\theta & =\frac{80}{x}\\ se{c}^2\theta \frac{d\theta }{dt}& =-\frac{80}{x^2}\frac{dx}{dt}\\ \frac{dx}{dt}& =-\frac{x^{2}se{c}^2\theta }{80}\times \frac{d\theta }{dt}\end{array}$

عندما x = 60 فإن: طول وتر المثلث القائم في الشكل أعلاه يساوي: $\sqrt{{60}^2+{80}^2}=100$

ومنه: $sec\theta =\frac{100}{60}=\frac{5}{3}$

إذن:

${\frac{dx}{dt}|}_{x=60}=-\frac{{60}^2\left(\frac{25}{9}\right)}{80}\times \frac{\pi }{720}=-\frac{25\pi }{144}\mathrm{m}/\min$

لتحويل الوحدة إلى cm/min نضرب السرعة في 100 ، فتكون:

${\frac{dx}{dt}|}_{x=60}=-\frac{2500\pi }{144}\mathrm{cm}/\min$

إذن يتناقص طول ظل البناية في تلك اللحظة بسرعة مقدارها 54.5 cm/min تقريباً.