طباعة الدرس

مسألة اليوم

المساحة

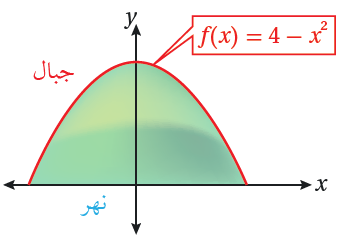يمثل الجزء المظلل بالأخضر في الشكل المجاور حقول منطقة زراعية تحيط بها سلسلة من الجبال، ويمثل منحنى الاقتران: f(x) = 4 – x² الحد الفاصل بين سلسلة الجبال والمنطقة الزراعية ويمثل المحور x حافة النهر الذي يطل على المنطقة الزراعية. أجد المساحة الكلية للمنطقة الزراعية علماً بأنّ x و y مقيساً بالكيلومتر.

f(x) = 4 – x²

أولاً نساوي قاعدة الاقتران بالصفر، ونحل المعادلة الناتجة:

$\begin{array}{rl}f\left(x\right)=0& \Rightarrow 4-x^2=0\\ & \Rightarrow (2+x)(2-x)=0\\ & \Rightarrow x=-2,x=2\end{array}$

وهي تمثل حدود التكامل.

$\begin{array}{rl}A& ={\int }_{-2}^2(4-x^2)dx\\ & ={(4x-\frac{1}{3}{x}^3)|}_{-2}^2\\ & =\left(4\right(2)-\frac{1}{3}(2{)}^3)-\left(4\right(-2)-\frac{1}{3}(-2{)}^3)\\ & =\frac{32}{3}\end{array}$

إذن المساحة هي: 10.667 كيلومتر مربع.