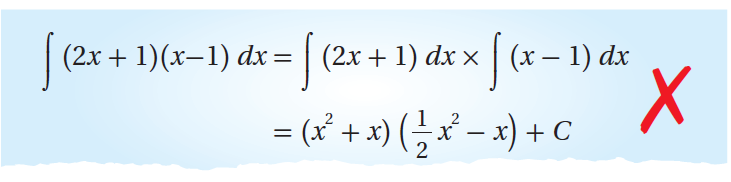مهارات التفكير العليا
التكامل غير المحدود
(20) أكتشف الخطأ: أوجدت رنيم ناتج التكامل: ، وكان حلها على النحو الآتي:
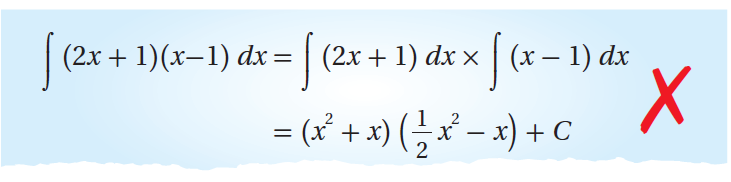
أكتشف الخطأ في حل رنيم، ثم أصححه.
تحدّ: أجد كل تكامل ممّا يأتي:
(21)
(22)
(23) تبرير: إذا كان: ، فأجد قيمة كلّ من الثابت P ، والثابت Q ، مبرراً إجابتي.