طباعة الدرس

مهارات التفكير العليا

التوزيع الطبيعي

(41) أكتشف الخطأ: قالت عبير: "إذا كان: $X~N(6.4,0.09)$، فإن %95 من البيانات تقع بين 6.22 و6.58". أكتشف الخطأ في قول عبير، ثم أصححه.

تقع %95 من البيانات بين $\mu +2\sigma , \mu -2\sigma$ (حسب القاعدة التجريبية)، وهذا يعني الفترة من 5.8 إلى 7 وليس الفترة التي ذكرتها عبير.

الخطأ الذي ارتكبته عبير، هو أنها اعتبرت $\sigma =0.09$ والصواب هو أن $\sigma =\sqrt{0.09}=0.3$.

(42) تبرير: إذا كان $P(X>35)=0.025,P(X<15)=0.1469,X~N(\mu ,{\sigma }^2)$، فأجد قيمة كل من $\mu ,\sigma$، مبرراً إجابتي.

$P(X<15)=P(Z<\frac{15-\mu }{\sigma })=0.1469$

نفرض أن $\frac{15-\mu }{\sigma }=z$ ، فيكون $P(Z<z)=0.1469$

الاحتمال المعطى (0.1469) يمثل المساحة التي تقع يسار القيمة z وهو أقل من 0.5، إذن: z سالبة

$\begin{array}{rl}& \Rightarrow P(Z<-z)=P(Z>z)\\ & 0.1469=1-P(Z<z)\\ & P(Z<z)=1-0.1469=0.8531\Rightarrow z=1.05\end{array}$

إذن، قيمة z التي تحقق الاحتمال المعطى هي 1.05-

$\begin{array}{rl}& \Rightarrow \frac{15-\mu }{\sigma }=-1.05\Rightarrow 15-\mu =-1.05\sigma \dots \dots \dots \dots \dots \dots \dots \left(1\right)\\ & P(X>35)=P(Z>\frac{35-\mu }{\sigma })=0.025\end{array}$

نفرض أن $\frac{35-\mu }{\sigma }=Z$، فيكون $P(Z>z)=0.025$

الاحتمال المعطى (0.025) يمثل المساحة التي تقع يمين القيمة z وهو أقل من 0.5، إذن: z موجبة

$\begin{array}{rl}& \Rightarrow P(Z<z)=1-P(Z>z)=1-0.025=0.975\\ & \Rightarrow z=1.96\Rightarrow \frac{35-\mu }{\sigma }=1.96\Rightarrow 35-\mu =1.96\sigma ........\left(2\right)\\ & \left(2\right)-\left(1\right): 20=3.01\sigma \Rightarrow \sigma \approx 6.64,\mu \approx 22\end{array}$

(43) تبرير: تقدم 100000 طالب لاختبار دولي، وبلغ عدد الطلبة الذين زادت علاماتهم في الاختبار على %90 نحو 10000 طالب، منهم 5000 طالب أحرزوا علامات أكثر من %95. إذا كانت علامات الطلبة المتقدمين تتبع توزيعاً طبيعياً، فأجد الوسط الحسابي، والانحراف المعياري للعلامات.

$P(X>90)=P(Z>\frac{90-\mu }{\sigma })=\frac{10000}{100000}=0.1$

نفرض أن $\frac{90-\mu }{\sigma }=Z$ ، فيكون $P(Z>z)=0.1$

الاحتمال المعطى (0.1) يمثل المساحة التي تقع يمين القيمة z وهو أقل من 0.5، إذن: z موجبة

$\begin{array}{rl}& \Rightarrow P(Z<z)=1-P(Z>z)=1-0.1=0.9\\ & \Rightarrow z=1.28\Rightarrow \frac{90-\mu }{\sigma }=1.28\Rightarrow 90-\mu =1.28\sigma .......\left(1\right)\\ & P(X>95)=P(Z>\frac{95-\mu }{\sigma })=\frac{5000}{100000}=0.05\end{array}$

نفرض أن $\frac{95-\mu }{\sigma }=z$، فيكون $P(Z>z)=0.05$

الاحتمال المعطى (0.05) يمثل المساحة التي تقع يمين القيمة z وهو أقل من 0.5، إذن: z موجبة

$$\begin{gathered} \begin{array}{rl}\Rightarrow P(Z<z)& =1-P(Z>z)\\ & =1-0.05=0.95\\ \Rightarrow z=1.64& \Rightarrow \frac{95-\mu }{\sigma }=1.64\Rightarrow 95-\mu =1.64\sigma .....\left(2\right)\end{array} \\ \left(2\right)-\left(1\right): 5=0.36\sigma \Rightarrow \sigma \approx 13.89,\mu \approx 72.22 \end{gathered}$$

(44) تحد: أجرت باحثة تفاعلاً كيميائياً بصورة متكررة، فوجدت أن الزمن اللازم لحدوث التفاعل يتبع توزيعاً طبيعياً، وأن %5 من التجارب يلزمها أكثر من 13 دقيقة لحدوث التفاعل، وأن %12 منها تتطلب أقل من 10 دقائق لحدوث التفاعل. أقدر الوسط الحسابي والانحراف المعياري لزمن التفاعل.

$P(X>13)=P(Z>\frac{13-\mu }{\sigma })=0.05$

نفرض أن $\frac{13-\mu }{\sigma }=Z$، فيكون $P(Z>z)=0.05$

الاحتمال المعطى (0.05) يمثل المساحة التي تقع يمين القيمة z وهو أقل من 0.5، إذن: z موجبة

$\begin{array}{rl}& \Rightarrow P(Z<z)=1-P(Z>z)=1-0.05=0.95\\ & \Rightarrow z=1.64\Rightarrow \frac{13-\mu }{\sigma }=1.64\Rightarrow 13-\mu =1.64\sigma ......\left(1\right)\\ & P(X<10)=P(Z<\frac{10-\mu }{\sigma })=0.12\end{array}$

نفرض أن $\frac{10-\mu }{\sigma }=Z$، فيكون $P(Z<z)=0.12$

الاحتمال المعطى (0.12) يمثل المساحة التي تقع يسار القيمة z وهو أقل من 0.5، إذن: z سالبة

$\begin{array}{r}\Rightarrow P(Z<-z)=1-P(Z<z)\\ 0.12=1-P(Z<z)\\ \Rightarrow P(Z<z)=0.88\Rightarrow z=1.17\end{array}$

إذن، قيمة z التي تحقق الاحتمال المعطى $P(Z<z)=0.12$ هي $z=-1.17$

$\begin{array}{rl}& \Rightarrow \frac{10-\mu }{\sigma }=-1.17\Rightarrow 10-\mu =-1.17\sigma ...........\left(2\right)\\ & \left(1\right)-\left(2\right): 3=2.81\sigma \Rightarrow \sigma \approx 1.07,\mu \approx 11.25\end{array}$ 

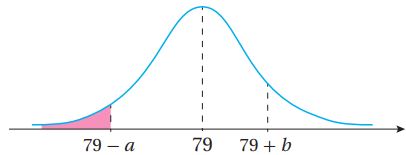تبرير: يبين الشكل المجاور منحنى التوزيع الطبيعي للمتغير العشوائي X الذي وسطه الحسابي 79، وتباينه 144. إذا كان: $\mathit{P}\mathbf{(}\mathbf{79}\mathbf{-}\mathit{a}\mathbf{\le }\mathit{X}\mathbf{\le }\mathbf{79}\mathbf{+}\mathit{b}\mathbf{)}\mathbf{=}\mathbf{0}\mathbf{.}\mathbf{6463}$ وكان: $\mathit{P}\mathbf{(}\mathit{X}\mathbf{\ge }\mathbf{79}\mathbf{+}\mathit{b}\mathbf{)}\mathbf{=}\mathbf{2}\mathit{P}\mathbf{(}\mathit{X}\mathbf{\le }\mathbf{79}\mathbf{-}\mathit{a}\mathbf{)}$ فأجد كلاً مما يأتي، مبرراً إجابتي:

(45) مساحة المنطقة المظللة.

المساحة الكلية تحت المنحى هي %100

المساحة تحت المنحنى بين القيمتين $79-a,79+b$ هي %64.63

إذن، المساحة تحت المنحنى خارج القيمتين $79-a,79+b$ هي: 

$100\mathrm{\%}-64.63\mathrm{\%}=35.37\mathrm{\%}$

وهي تمثل منطقتين إحداهما مساحتها ضعف الأخرى (حسب المعطى)، فتكون مساحة المنطقة المظللة تساوي $\frac{35.37\mathrm{\%}}{3}=11.79\mathrm{\%}$

أو نكتب:

$$\begin{gathered} \begin{array}{rl}& P(79-a\le X\le 79+b)=P(X\le 79+b)-P(X\le 79-a)\\ & \Rightarrow P(X\le 79+b)-P(X\le 79-a)=0.6463\dots \dots \dots \dots \dots \left(1\right)\\ & P(X\ge 79+b)=2P(X\le 79-a)\end{array} \\ \begin{array}{rl}& \Rightarrow 1-P(X<79+b)=2P(X\le 79-a)\\ & \Rightarrow P(X<79+b)+2P(X\le 79-a)=1.........\left(2\right)\\ & \text{(2)}-\left(1\right)\Rightarrow 3P(X\le 79-a)=0.3537\\ & \Rightarrow P(X\le 79-a)=0.1179,P(X\ge 79+b)=0.2358\end{array} \end{gathered}$$

إذن، مساحة المنطقة المظللة تساوي: $P(X\le 79-a)=0.1179$

(46) قيمة الثابت b.

وجدنا في السؤال السابق أن:

$\begin{array}{rl}& P(X\ge 79+b)=0.2358\\ & \Rightarrow P(Z\ge \frac{79+b-79}{12})=0.2358\\ & \Rightarrow P(Z\ge \frac{b}{12})=0.2358\end{array}$

نفرض أن $\frac{b}{12}=z$، فيكون:

$\begin{array}{c}P(Z\ge z)=0.2358\\ \Rightarrow P(Z<z)=1-0.2358=0.7642\\ \Rightarrow z=0.72\Rightarrow \frac{b}{12}=0.72\Rightarrow b=8.64\end{array}$