مهارات التفكير العليا

مهارات التفكير العليا

التكامل بالتعويض

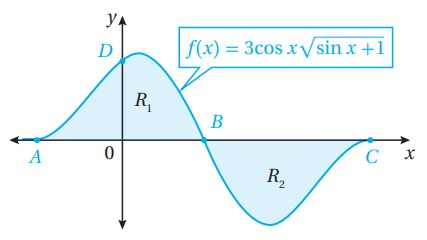تبرير: إذا كان الشكل المجاور بمثل منحنى الاقتران: $f (x) = 3 c o s x \sqrt{s i n x + 1}$ ، فأجيب عن الأسئلة الآتية تباعاً:

(40) أجد إحداثيي كل من النقاط: $A, B, C, D$ .

$\begin{aligned} f (x) = 0 \Rightarrow 3 \cos x \sqrt{1 + \sin x} = 0 \\ \cos x = 0 \Rightarrow x = \frac{π}{2} + 2 n π, n \in ℤ, x = \frac{3 π}{2} + 2 n π, n \in ℤ \\ \sin x = - 1 \Rightarrow x = \frac{3 π}{2} + 2 n π, n \in ℤ \end{aligned}$

يوجد عدد لا نهائي من الحلول لهاتين المعادلتين، نريد أصغر حلين موجبين (الإحداثي $x$ للنقطتين $C, B$ ) وأكبر حل ساالب (الإحداثي $x$ للنقطة $A$ ).

أصغر حلين موجبين هما: $x = \frac{π}{2}, x = \frac{3 π}{2}$ ، بوضع $n = 0$

$\Rightarrow B (\frac{π}{2}, 0), C (\frac{3 π}{2}, 0)$

أكبر حل سالب هو: $x = - \frac{π}{2}$ ، بوضع $n = - 1$

$⟹ A (- \frac{π}{2}, 0)$

أما النقطة $D$ فإحداثياها هما: $D (0, f (0)) = (0, 3)$

(41) أجد مساحة المنطقة المظللة.

$\begin{aligned} A = A_{1} + A_{2} = A (R_{1}) + A (R_{2}) \\ A = \int_{- \frac{π}{2}}^{\frac{π}{2}} (3 \cos x \sqrt{1 + \sin x}) d x + (- \int_{\frac{π}{2}}^{\frac{3 π}{2}} (3 \cos x \sqrt{1 + \sin x}) d x) \\ u = 1 + \sin x \Rightarrow \frac{d u}{d x} = \cos x \Rightarrow d x = \frac{d u}{\cos x} \\ x = - \frac{π}{2} \Rightarrow u = 0 \\ x = \frac{π}{2} \Rightarrow u = 2 \\ x = \frac{3 π}{2} \Rightarrow u = 0 \\ A = 3 \int_{0}^{2} \cos x \sqrt{u} \frac{d u}{\cos x} + (- 3 \int_{2}^{0} \cos x \sqrt{u} \frac{d u}{\cos x}) \\ = 3 \int_{0}^{2} \sqrt{u} d u + 3 \int_{0}^{2} \sqrt{u} d u \\ = 6 \int_{0}^{2} \sqrt{u} d u = {4 u^{\frac{3}{2}} |}_{0}^{2} = 4 (2 \sqrt{2} - 0) = 8 \sqrt{2} \end{aligned}$

(42) أبين أن للمنطقة $R_{1}$ والمنطقة $R_{2}$ المساحة نفسها.

من حل السؤال السابق نجد أن:

$\begin{aligned} A (R_{1}) = \int_{- \frac{π}{2}}^{\frac{π}{2}} (3 \cos x \sqrt{1 + \sin x}) d x = \int_{0}^{2} 3 \sqrt{u} d u = 4 \sqrt{2} \\ A (R_{2}) = - \int_{\frac{π}{2}}^{\frac{3 π}{2}} (3 \cos x \sqrt{1 + \sin x}) d x = - \int_{2}^{0} 3 \sqrt{u} d u = 4 \sqrt{2} \\ \Rightarrow A (R_{1}) = A (R_{2}) \end{aligned}$

(43) تحد: أجد قيمة: $\int_{1}^{16} \frac{\sqrt{x}}{1 + \sqrt[4]{x^{3}}} d x$ .

$\begin{aligned} u = 1 + x^{\frac{3}{4}} \Rightarrow \frac{d u}{d x} = \frac{3}{4} x^{- \frac{1}{4}} \Rightarrow d x = \frac{4}{3} x^{\frac{1}{4}} d u, x^{\frac{3}{4}} = u - 1 \\ x = 1 \Rightarrow u = 2 \\ x = 16 \Rightarrow u = 9 \\ \int_{1}^{16} \frac{\sqrt{x}}{1 + \sqrt[4]{x^{3}}} d x = \int_{2}^{9} \frac{x^{\frac{1}{2}}}{u} \frac{4}{3} x^{\frac{1}{4}} d u \\ = \frac{4}{3} \int_{2}^{9} \frac{x^{\frac{3}{4}}}{u} d u = \frac{4}{3} \int_{2}^{9} \frac{u - 1}{u} d u = \frac{4}{3} \int_{2}^{9} (1 - \frac{1}{u}) d u \\ = {\frac{4}{3} (u - \ln | u |) |}_{2}^{9} = \frac{4}{3} (7 - \ln \frac{9}{2}) \end{aligned}$

(44) تبرير: إذا كان $f$ اقتراناً متصلاً، فأثبت أن: $\int_{0}^{π / 2} f (\cos x) d x = \int_{0}^{π / 2} f (\sin x) d x$ .

$\begin{aligned} \int_{0}^{\frac{π}{2}} f (\cos x) d x = \int_{0}^{\frac{π}{2}} f (\sin (\frac{π}{2} - x)) d x \\ u = \frac{π}{2} - x \Rightarrow d x = - d u \\ x = 0 \Rightarrow u = \frac{π}{2} \\ x = \frac{π}{2} \Rightarrow u = 0 \\ \int_{0}^{\frac{π}{2}} f (\cos x) d x = \int_{\frac{π}{2}}^{0} - f (\sin u) d u = \int_{0}^{\frac{π}{2}} f (\sin u) d u = \int_{0}^{\frac{π}{2}} f (\sin x) d x \end{aligned}$

(45) تبرير: إذا كان $a, b$ عددين حقيقيين موجبين، فأثبت أن: $\int_{0}^{1} x^{a} (1 - x)^{b} d x = \int_{0}^{1} x^{b} (1 - x)^{a} d x$ .

$b b b$

تحد: أجد كلاً من التكاملات الآتية:

$\int \frac{d x}{x \ln x (\ln (\ln x))}$ (46)

$b b b$

$\int \frac{\sin x - \cos x}{\sin x + \cos x} d x$ (47)

$b b b$

$\int \sin 2 x (1 + \sin x)^{3} d x$ (48)

$b b b$