طباعة الدرس

مهارات التفكير العليا

تكامل اقترانات خاصة

تبرير: أجد مساحة المنطقة المظللة في كل من التمثيلين البيانيين الآتيين، مبرراً إجابتي;

$\begin{array}{rl}& \sin x=0\Rightarrow x=0,\pi ,2\pi \\ & A={\int }_0^{\pi }\sin xdx+(-{\int }_{\pi }^{2\pi }\sin xdx)={(-\cos x)|}_0^{\pi }+{(\cos x)|}_{\pi }^{2\pi }\\ & =-\cos \pi +\cos 0+\cos 2\pi -\cos \pi =4\end{array}$

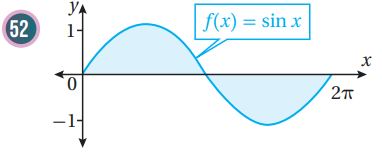
ملحوظة: يمكن الاستفادة من التماثل وإيجاد المساحة المطلوبة كما يأتي:

$A=2{\int }_0^{\pi }\sin xdx={2(-\cos x)|}_0^{\pi }=2(-\cos \pi +\cos 0)=2\left(2\right)=4$

$\begin{array}{rl}& \sin 2x=0\Rightarrow x=0,\frac{\pi }{2},\pi ,\frac{3\pi }{2},2\pi \\ & A={\int }_0^{\frac{\pi }{2}}\sin 2xdx+(-{\int }_{\frac{\pi }{2}}^{\pi }\sin 2xdx)+{\int }_{\pi }^{\frac{3\pi }{2}}\sin 2xdx\\ & +(-{\int }_{\frac{3\pi }{2}}^{2\pi }\sin 2xdx)\end{array}$

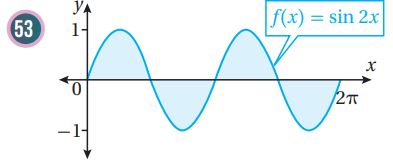
والأسهل هو الاستفادة من التماثل وإيجاد المساحة المطلوبة كما يأتي:

$A=4{\int }_0^{\frac{\pi }{2}}\sin 2xdx=-{2\cos 2x|}_0^{\frac{\pi }{2}}=-2(-1-1)=4$

تحد: أجد كلاً من التكاملات الآتية:

$\int \frac{\sec x}{\sin x-\cos x}dx$ (54)

$\begin{array}{rl}\int \frac{\sec x}{\sin x-\cos x}dx& =\int \frac{\frac{\sec x}{\cos x}}{(\frac{\sin x}{\cos x}-1)}dx\\ & =\int \frac{{\sec }^{2}x}{(\tan x-1)}dx\\ & =\ln |\tan x-1|+C\end{array}$

$\int \frac{\cot x}{2+\sin x}dx$ (55)

$\begin{array}{rl}\int \frac{\cot x}{2+\sin x}dx& =\int \frac{\cot x\csc x}{2\csc x+1}dx\\ & =-\frac{1}{2}\int \frac{-2\cot x\csc x}{2\csc x+1}dx\\ & =-\frac{1}{2}\ln |2\csc x+1|+C\\ & =-\frac{1}{2}\ln |2\csc x+1|+C\end{array}$

$\int \frac{1}{x\ln x^3}dx$ (56)

$\int \frac{1}{x\ln x^3}dx=\int \frac{1}{3x\ln x}dx=\frac{1}{3}\int \frac{\frac{1}{x}}{\ln x}dx=\frac{1}{3}\ln |\ln x|+C$

(57) تبرير: إذا كان: ${\int }_1^a(\frac{1}{x}-\frac{1}{2x+3})dx=0.5\ln 5$، فأجد قيمة الثابت a، حيث: $a>0$.

$$\begin{gathered} \begin{array}{rl}{\int }_1^a(\frac{1}{x}-\frac{1}{2x+3})dx& ={(ln|x|-\frac{1}{2}ln|2x+3\left|\right)|}_1^a\\ & =(lna-\frac{1}{2}ln(2a+3\left)\right)-(-\frac{1}{2}ln5)\\ & =lna-\frac{1}{2}ln(2a+3)+\frac{1}{2}ln5\\ & =ln\frac{a}{\sqrt{2a+3}}+\frac{1}{2}ln5\end{array} \\ \begin{array}{rl}& \Rightarrow ln\frac{a}{\sqrt{2a+3}}+\frac{1}{2}ln5=0.5ln5\\ & \Rightarrow ln\frac{a}{\sqrt{2a+3}}=0\\ & \Rightarrow \frac{a}{\sqrt{2a+3}}=1\\ & \Rightarrow a=\sqrt{2a+3}\\ & \Rightarrow a^2=2a+3\\ & \Rightarrow a^2-2a-3=0\\ & \Rightarrow (a-3)(a+1)=0\\ & \Rightarrow a=3,a=-1\left(a>0 \mathrm{لأن} \mathrm{مرفوضة}\right)\end{array} \end{gathered}$$

(58) تبرير: أثبت بطريقتين مختلفتين أن: ${\int }_0^{\pi /4}\cos x\cos 3xdx-{\int }_0^{\pi /4}\sin x\sin 3xdx=0$.

طريقة أولى: 

$$\begin{gathered} \begin{array}{rl}{\int }_0^{\frac{\pi }{4}}\cos x\cos 3xdx& =\frac{1}{2}{\int }_0^{\frac{\pi }{4}}(\cos 4x+\cos 2x)dx\\ & ={(\frac{1}{8}\sin 4x+\frac{1}{4}\sin 2x)|}_0^{\frac{\pi }{4}}\\ & =(\frac{1}{8}\sin \pi +\frac{1}{4}\sin \frac{\pi }{2})-(0+0)=\frac{1}{4}\dots \dots \dots ..\left(1\right)\end{array} \\ \begin{array}{rl}& {\int }_0^{\frac{\pi }{4}}\sin x\sin 3xdx=\frac{1}{2}{\int }_0^{\frac{\pi }{4}}(\cos 2x-\cos 4x)dx\\ & ={(\frac{1}{4}\sin 2x-\frac{1}{8}\sin 4x)|}_0^{\frac{\pi }{4}}\\ & =(\frac{1}{4}\sin \frac{\pi }{2}-\frac{1}{8}\sin \pi )-(0-0)=\frac{1}{4}\dots \dots \dots \dots \left(2\right)\\ & \Rightarrow {\int }_0^{\frac{\pi }{4}}\cos x\cos 3xdx-{\int }_0^{\frac{\pi }{4}}\sin x\sin 3xdx=\frac{1}{4}-\frac{1}{4}=0\end{array} \end{gathered}$$

طريقة ثانية:

$\begin{array}{rl}& {\int }_0^{\frac{\pi }{4}}\cos x\cos 3xdx-{\int }_0^{\frac{\pi }{4}}\sin x\sin 3xdx\\ & ={\int }_0^{\frac{\pi }{4}}(\cos x\cos 3x-\sin x\sin 3x)dx={\int }_0^{\frac{\pi }{4}}\cos (x+3x)dx\\ & ={\int }_0^{\frac{\pi }{4}}\cos 4xdx={\frac{1}{4}\sin 4x|}_0^{\frac{\pi }{4}}=\frac{1}{4}(\sin \pi -\sin 0)=0\end{array}$

(59) تبرير: إذا كان: ${\int }_{\pi /4k}^{\pi /3k}(1-\pi \sin kx)dx=\pi (7-6\sqrt{2})$، فأجد قيمة الثابت k، مبرراً إجابتي.

$\begin{array}{rl}& {\int }_{\frac{\pi }{4k}}^{\frac{\pi }{3k}}(1-\pi \sin kx)dx={(x+\frac{\pi }{k}\cos kx)|}_{\frac{\pi }{4k}}^{\frac{\pi }{3k}}\\ & =\frac{\pi }{3k}+\frac{\pi }{k}\cos \frac{\pi }{3}-\frac{\pi }{4k}-\frac{\pi }{k}\cos \frac{\pi }{4}\\ & =\frac{\pi }{k}(\frac{1}{3}+\frac{1}{2}-\frac{1}{4}-\frac{\sqrt{2}}{2})=\frac{\pi }{12k}(7-6\sqrt{2})\\ & \Rightarrow \frac{\pi }{12k}(7-6\sqrt{2})=\pi (7-6\sqrt{2})\\ & \Rightarrow k=\frac{1}{12}\end{array}$

تحد: يتحرك جسيم في مسار مستقيم، وتعطى سرعته المتجهة بالاقتران:

$\mathit{v}\mathbf{\left(}\mathit{t}\mathbf{\right)}\mathbf{=}\mathbf{\{}\begin{array}{ll}\mathbf{2}\mathbf{t}\mathbf{+}\mathbf{4}& \mathbf{,}\mathbf{0}\mathbf{\le }\mathbf{t}\mathbf{\le }\mathbf{6}\\ \mathbf{20}\mathbf{-}\mathbf{(}\mathbf{t}\mathbf{-}\mathbf{8}{\mathbf{)}}^{\mathbf{2}}& \mathbf{,}\mathbf{6}\mathbf{<}\mathbf{t}\mathbf{\le }\mathbf{10}\end{array}$

حيث t الزمن بالثواني، وv سرعته المتجهة بالمتر لكل ثانية. إذا بدأ الجسيم حركته من نقطة الأصل، فأجد كلاً مما يأتي:

(60) موقع الجسيم بعد 5 ثوان من بدء الحركة.

$$\begin{gathered} \begin{array}{rl}& v\left(t\right)=\{\begin{array}{cc}2t+4,& 0\le t\le 6\\ 16t-t^2-44,& 6<t\le 10\end{array}\\ & s\left(t\right)=\int v\left(t\right)dt\end{array} \\ \begin{array}{rl}& s\left(t\right)=\int (2t+4)dt=t^2+4t+C_1 \left(0\le t\le 6 \mathrm{عندما}\right)\\ & s\left(0\right)=0\Rightarrow C_1=0\\ & \Rightarrow s\left(t\right)=t^2+4t,0\le t\le 6\\ & s\left(5\right)=25+20=45\mathrm{m}\end{array} \end{gathered}$$

(61) موقع الجسيم بعد 9 ثوان من بدء الحركة.

$s\left(t\right)=\int (16t-t^2-44)dt=8t^2-\frac{1}{3}{t}^3-44t+C_2 \left(6<t\le 10 \mathrm{عندما}\right)$

لإيجاد قيمة ${\mathrm{C}}_2$ نستعمل موقع الجسم عند $t=6$ موقعاً ابتدائياً بالنسبة للفترة $\left[6,10\right]$:

$s\left(6\right)=8(6{)}^2-\frac{1}{3}(6{)}^3-44\left(6\right)+C_2$

ونحسب $s\left(6\right)$ من اقتران الموقع الذي وجدناه في السؤال السابق بالنسبة للفترة $[0,6]$:

$\begin{array}{rl}& s\left(t\right)=t^2+4t,0\le t\le 6\\ & s\left(6\right)=6^2+4\left(6\right)=60\\ & 60=8(6{)}^2-\frac{1}{3}(6{)}^3-44\left(6\right)+C_2\\ & 60=-48+C_2\Rightarrow C_2=108\\ & \Rightarrow s\left(t\right)=8t^2-\frac{1}{3}{t}^3-44t+108,6<t\le 10\\ & s\left(9\right)=117\mathrm{m}\end{array}$

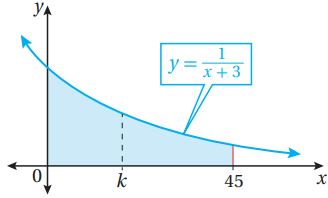(62) تحد: يبين الشكل المجاور المنطقة المحصورة بين منحنى الاقتران: $y=\frac{1}{x+3}$، والمحـور x، والمستقيمين: $x=45,،x=0$ أجد قيمة k التي تقسم المنطقة المطلقة إلى منطقتين متساويتين في الساحة.

$\begin{array}{rl}& \begin{array}{rl}A={\int }_0^{45}\frac{1}{x+3}dx& =ln\mid x+3{\parallel }_0^{45}\\ & =ln48-ln3=ln16\\ \frac{1}{2}A={\int }_0^k\frac{1}{x+3}dx& =ln\mid x+3{\parallel }_0^k\\ & =ln(k+3)-ln3\\ & =ln\frac{k+3}{3}\end{array}\\ & \begin{array}{r}\Rightarrow \frac{1}{2}ln16=ln\frac{k+3}{3}\end{array}\\ & ln16\frac{1/2}{}=ln\frac{k+3}{3}\\ & \Rightarrow 4=\frac{k+3}{3}\Rightarrow k=9\end{array}$