 |
أتدرب وأحل المسائل
تمثيل الاقتران الخطي بيانياً
أكمل الجدول، ثم أمثل الاقتران بيانياً في كلّ ممّا يأتي:
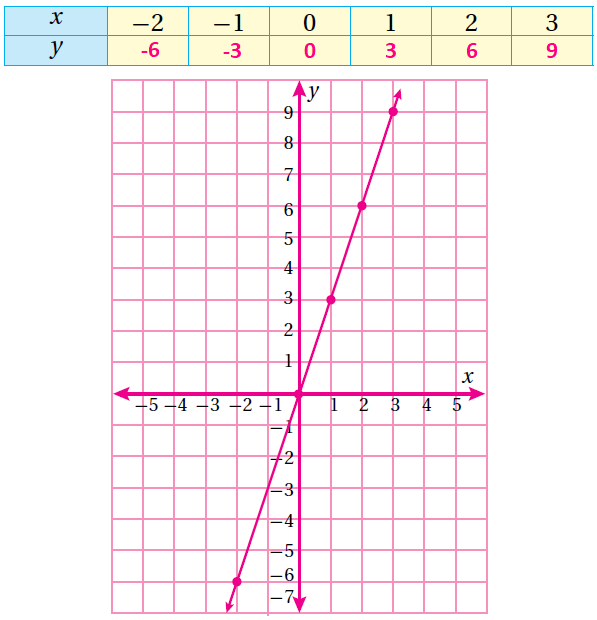
(1) y = 3x
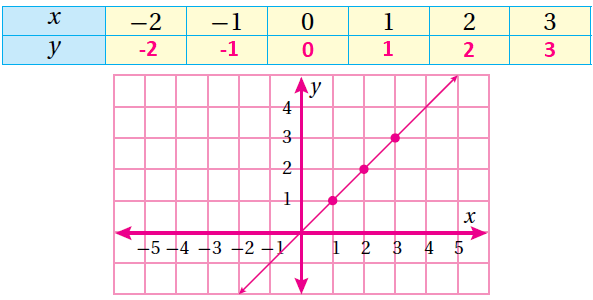
(2) y = x
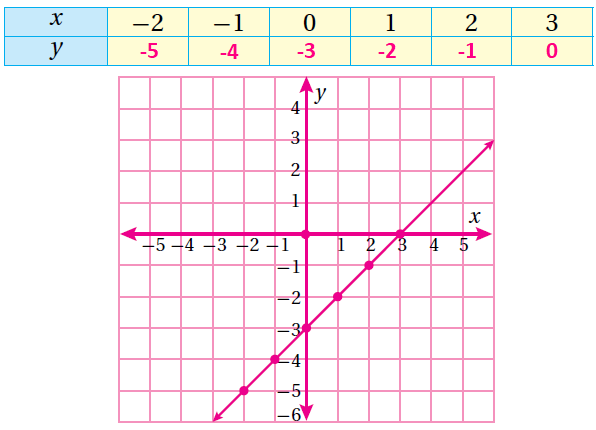
(3) y = x - 3
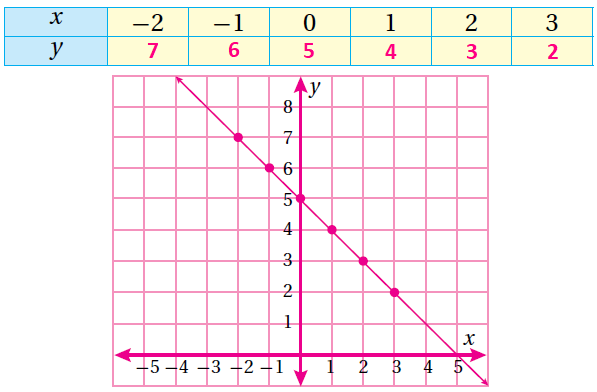
(4) y = 5 - x
أجد أربعة حلول لكلّ معادلة مما يأتي ثم أمثلها بيانياً على المستوى الإحداثي.
(5) y = 3x + 1
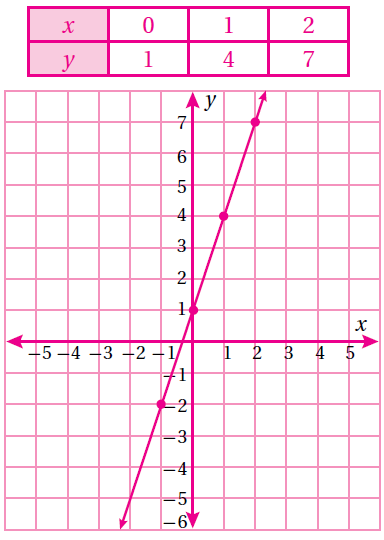
(6) y = 4x - 3
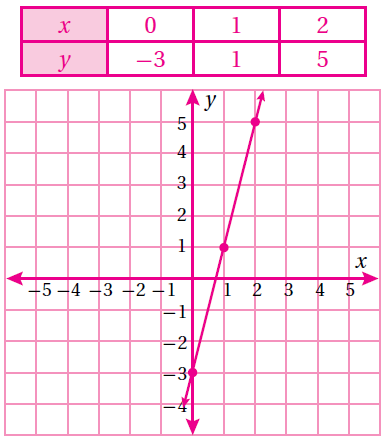
(7) y = 3 – 2x
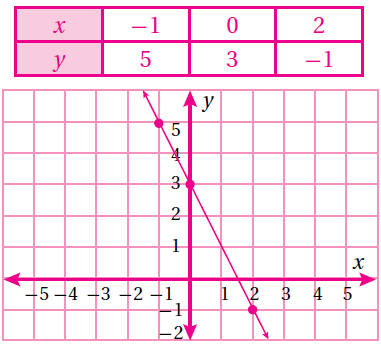
(8) y = 2x – 5
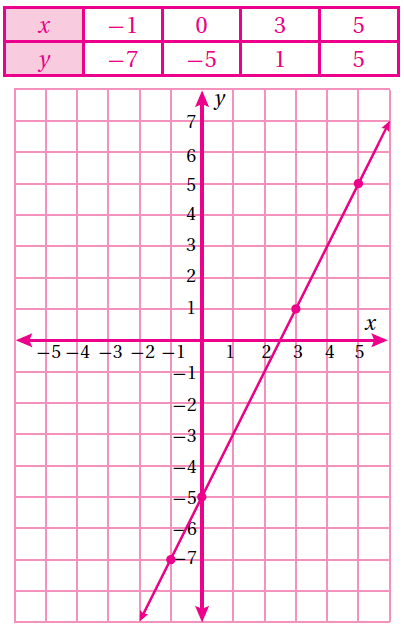
(9) y = 4 – 3x
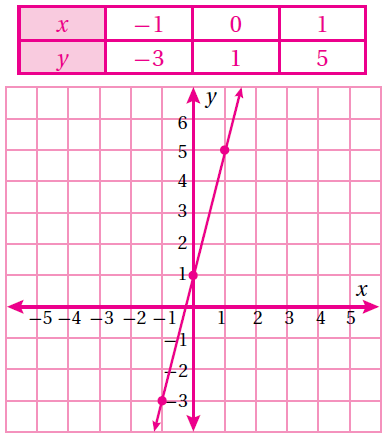
(10) y = 4x + 1
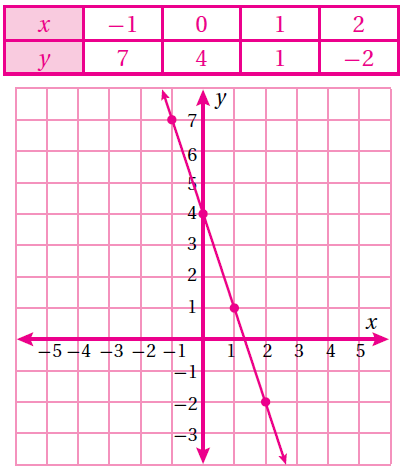
(11) أي أزواج الإحداثيات الآتية يقع على المستقيم الذي معادلته y = 2x - 3 ؟ أبرر إجابتي.
a) (2, 7) b) (-1, 05) c) (15, 27)
النقطة a لا تقع على المستقيم؛ لأنه عند تعويض قيمة x و y في معادلة المستقيم:
7 = 2(2) - 3
7 ≠ -1الطرف الأيمن لا يساوي الطرف الأيسر.
إذن النقطة a لا تحقق معادلة المستقيم.
النقطة b تقع على المستقيم وذلك عند تعويض قيمة x و y في معادلة المستقيم:
-5 = 2(-1) - 3
-5 = -5 الطرفان متساويان.
إذن النقطة b تحقق معادلة المستقيم.
النقطة c تقع على المستقيم وذلك عند تعويض قيمة x و y في معادلة المستقيم:
27 = 2(15) - 3
27 = 27 الطرفان متساويان.
إذن النقطة c تحقق معادلة المستقيم.
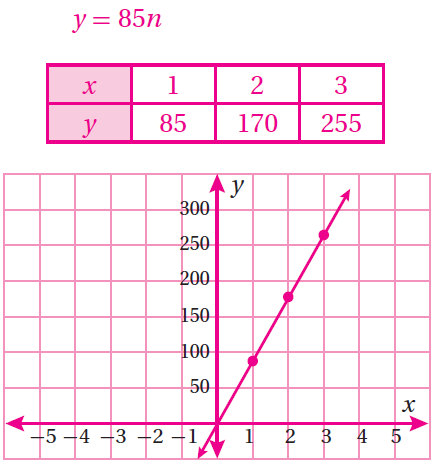
(12) قطارات: تتسع العربة الواحدة في قطار إلى 85 راكباً. أكتب اقتراناً يمثل عدد الركاب الذين يسعهم أيّ عدد من عربات القطار، ثم أمثل الاقتران بيانياً.
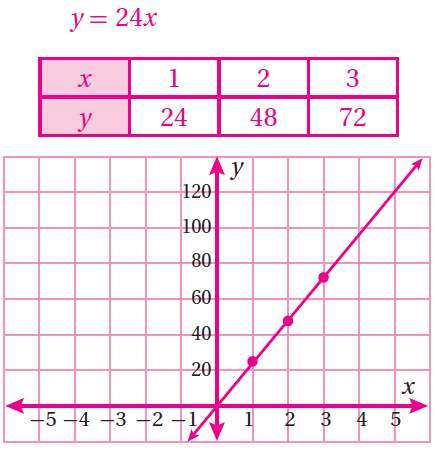
(13) مهن: يصنع نجارٌ كلّ يومٍ 6 طاولاتٍ لكلّ منها 4 أرجل. أكتب معادلة في متغيرين تمثل عدد أرجل الطاولات التي يصنعها النجّار بعد مرور عدد من الأيام ثم أمثّل المعادلة بيانياً.
(14) مشتريات: إذا كان ثمن الحقيبة الواحدة JD 10 وثمن القميص الواحد JD 7 فأكتب اقتراناً يمثل ثمن حقيبة واحدة وعدد من القمصان.
y = 7x + 10
أستخدم التمثيل البياني الآتي:
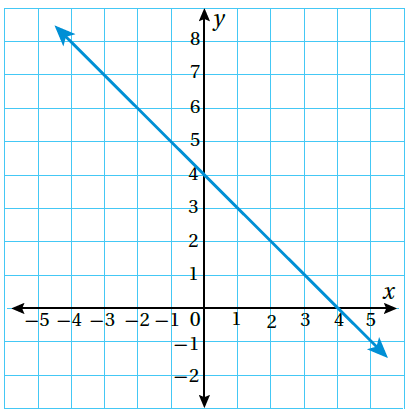
(15) أجد قيمة المدخلة x التي تقابل كل مخرجة ممّا يأتي:
y = 6 , y = 0 , y = 3
(-2, 6) , (4, 0) , (1, 3)
(16) أكتب المعادلة التي تمثل المستقيم.
y = -x + 4
يمكن حساب الحدّ الأقصى لمعدّل ضربات قلب الإنسان (y) في الدقيقة في أثناء ممارسته الرياضة بالمعادلة: y = 208 – 0.7x ، حيث x العمر بالسنوات
(17) ما الحدّ الأقصى لمعدّل ضربات قلب شخص عمره 30 سنة، وآخر عمره 50 سنة؟
الحد الأقصى لضربات قلب شخص عمره 30 سنة: 187 نبضة.
الحد الأقصى لضربات قلب شخص عمره 50 سنة: 194 نبضة.
(18) ما عمر شخص معدّل ضربات قلبه 194 نبضة في الدقيقة؟
20 سنة.
(19) هل معدّل ضربات القلب يزداد أم ينقص مع العمر؟ أبرر إجابتي.
ينقص؛ لأن النشاط البدني للإنسان يقل مع التقدم في العمر.
(20) أمثل المعادلة بيانياً.
