طباعة الدرس

أتدرب وأحل المسائل

الاقترانات الأسية

أجد قيمة كل اقتران ممّا يأتي عند قيمة x المعطاة:

(1) f(x) = (11)^x , x = 3

f(3) = (11)³ = 1331

(2) f(x) = -5(2)^x , x = 1

f(1) = -5(2)¹ = -5(2) = -10

(3) f(x) = 3($\frac{1}{7}$)^x , x = 2

f(2) = 3($\frac{1}{7}$)² = 3($\frac{1}{49}$) = $\frac{3}{49}$

(4) f(x) = -(5)^x + 4 , x = 4

f(4) = -(5)⁴ + 4 = -(625) + 4 = -621

(5) f(x) = 3^x + 1 , x = 5

f(5) = (3)⁵ + 1 = 243 + 1 = 244

(6) f(x) = ($\frac{1}{9}$)^x - 3 , x = 2

f(2) = ($\frac{1}{9}$)² - 3 = $\frac{1}{81}$ - 3 = $\frac{1}{81}$ - $\frac{243}{81}$ = - $\frac{242}{81}$

 

أمثل كل اقتران ممّا يأتي بيانياً، ثم أجد مجاله ومداه:

(7) f(x) = 4^x

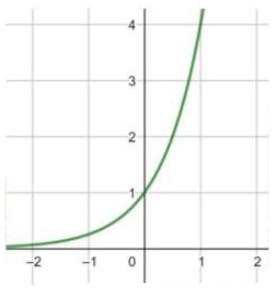
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية R .

مدى هذا الاقتران هو (0 , $\infty$).

(8) f(x) = 9^-x

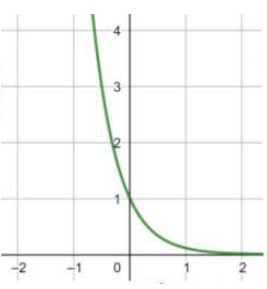
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية R .

مدى هذا الاقتران هو (0 , $\infty$).

(9) f(x) = 7($\frac{1}{7}$)^x

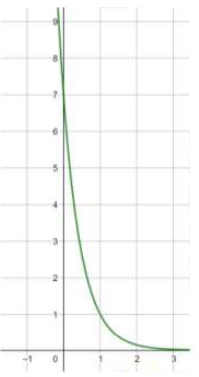
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية R .

مدى هذا الاقتران هو (0 , $\infty$).

(10) f(x) = 3(6)^x

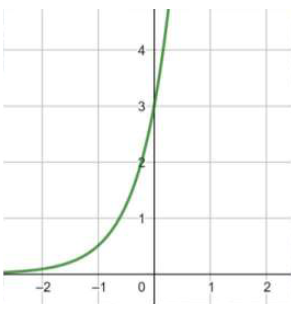
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية R .

مدى هذا الاقتران هو (0 , $\infty$).

 

أجد خط التقارب الأفقي لكل اقتران ممّا يأتي، ثم أحدد مجاله ومداه، مبيناً إذا كان متناقصاً أم متزايداً:

(11) f(x) = 5^x-1 + 2

لهذا الاقتران خط تقارب أفقي هو y = 2

مجال هذا الاقتران هو مجموعة الأعداد الحقيقية R .

مدى هذا الاقتران هو ($\infty$2 , ).

الاقتران f(x) متزايد.

(12) f(x) = ($\frac{1}{4}$)^x+2 - 5

لهذا الاقتران خط تقارب أفقي هو y = -5

مجال هذا الاقتران هو مجموعة الأعداد الحقيقية R .

مدى هذا الاقتران هو ($\infty$-5 , ).

الاقتران f(x) متناقص.

(13) f(x) = 3($\frac{1}{7}$)^x+5 - 6

لهذا الاقتران خط تقارب أفقي هو y = -6

مجال هذا الاقتران هو مجموعة الأعداد الحقيقية R .

مدى هذا الاقتران هو ($\infty$-6 , ).

الاقتران f(x) متناقص.

(14) f(x) = 3(7)^x-2 + 1

لهذا الاقتران خط تقارب أفقي هو y = 1

مجال هذا الاقتران هو مجموعة الأعداد الحقيقية R .

مدى هذا الاقتران هو ($\infty$1 , ).

الاقتران f(x) متزايد.

 

بكتيريا: يمثل الاقتران:f(x) = 7000(1.2)^x  عدد الخلايا البكتيرية في تجربة مخبرية، حيث x الزمن بالساعات:

(15) أجد عدد الخلايا البكتيرية في بداية التجربة.

f(0) = 7000(1.2)⁰ = 7000(1) = 7000

عدد الخلايا البكتيريا 70000 خلية.

(16) أجد عدد الخلايا البكتيرية بعد 12 ساعة.

f(12) = 7000(1.2)¹²  ≈ 62413

 عدد الخلايا البكتيرية بعد 12 ساعة هو 62413 خلية تقريباً.

(17) بعد كم ساعة يصبح عدد الخلايا البكتيرية 10080 خلية؟

10080 = 7000(1.2)^x 

1.44 = (1.2)^x

(1.2)² = (1.2)^x

x = 2

يصبح عدد الخلايا البكتيرية 10080 بعد ساعتين من بدء التجربة.

 

ضوء: يمثل الاقتران:f(x) = 100(0.97)^x  النسبة المئوية للضوء المار خلال x من الألواح الزجاجية المتوازية:

(18) أجد النسبة المئوية للضوء المار خلال لوح زجاجي واحد.

f(1) = 100(0.97)¹ = 100(0.97) = 97

نسبة الضوء المار خلال لوح زجاجي واحد هي 97%

(19) أجد النسبة المئوية للضوء المار خلال 3 ألواح زجاجية.

f(3) = 100(0.97)³ ≈ 91

نسبة الضوء المار خلال 3 ألواح زجاجية هي 91%

 

سرطان البنكرياس: يمثل الاقتران:P(t) = 100(0.3)^t  النسبة المئوية للمتعافين من مرضى سرطان البنكرياس، ممن هم في المرحلة المتقدمة، حيث تعافوا بعد t سنة من التشخيص الأوليّ للمرض:

(20) أجد النسبة المئوية للمتعافين بعد سنة من التشخيص الأولي للمرض.

P(1) = 100(0.3)¹ = 100(0.3) = 30

نسبة المتعافين بعد سنة من التشخيص الأوليّ هي 30%

(21) بعد كم سنة تصبح النسبة المئوية للمتعافين 9% ؟

9 = 100(0.3)^t

0.09 = (0.3)^t

(0.3)² = (0.3)^t

t = 2

بعد سنتين تصبح نسبة المتعافين 9%